CFA-01

于 2024-04-16 发布

利率有三种理解：

  1. 要求的回报率
  2. discount rates
  3. 机会成本

r = Real risk-free interest rate + Inflation premium + Default risk premium + Liquidity premium + Maturity premium.

理论上：(1 + nominal risk-free rate) = (1 + real risk-free rate)(1 + inflation premium)

实际上简化为：Nominal risk-free rate = Real risk-free rate + inflation premium

金融资产的收益有两部分：1）现金分红或利息支付；2）价格波动的收益。

平均数和持有收益率

普通的holding period return是：

$$ R=[(1+R_1)\times(1+R_2)\times...\times(1+R_n)]-1 $$

平均收益率有数学平均和几何平均，几何平均是：

$$ \bar R_{Gi}=\sqrt[T]{(1+R_{i1})\times (1+R_{i2})\times ...\times(1+R_{iT})}-1\\ =\sqrt[T]{\pi_{t=1}^T{(1+R_{it})}}-1 $$

通常来说数学平均会高估，除非底层回报率都是相同的。

几何平均表现出了compouding 的特性，在多周期的报告上比较有用；数学平均则对于单周期比较有用。

Harmonic mean：

$$ \bar X_H=\frac{n}{\Sigma(1/X_i)},\text{ }X_i>0 $$

如果data是rates或者ratios（比如P/E）会比较有用，极端值影响较少。特别是对于base固定但是ratio不同的情况有用，比如cost averaging（例如定投）。

image-20240416181608154

$ 数学平均\times Harmonic平均={几何平均}^2 $

而且 $ H平均 < 几何平均 < 数学平均 $

trimmed平均：去掉最大去掉最小

winsorized平均：上下限替换。

money加权和时间加权回报

money加权收益率就是IRR：

$$ \Sigma_{t=0}^T\frac{ {CF}_t}{1+{IRR}^t}=0 $$

因为不同时间投入不同的钱造成的加权不一样，所以遇到比较的时候不太能用。

时间加权，特点是对于现金的投入和赎回不敏感，有三步：

  1. Price the portfolio immediately prior to any significant addition or withdrawal of funds。根据投入或赎回的时间切分成sub-period
  2. 计算每个period的holding period return
  3. Link or compound holding period returns to obtain an annual rate of return for the year。如果时间超过1年，用几何平均来获取年回报率。

第一步在实际里很难做，但是如果组合是being valued frequent, regular intervals， particularly if additions and withdrawals are unrelated to market movements，那这个近似值就会很精准。比如365天天天定价，那就可以先算每天的持有收益率，然后 $ (1+R_1)\times(1+R_2)\times…\times (1+R_{365})-1 $ 得到时间加权年回报率。如果不止1年，那就先算每个年的时间加权年回报率，再几何平均。

例如以下例子：

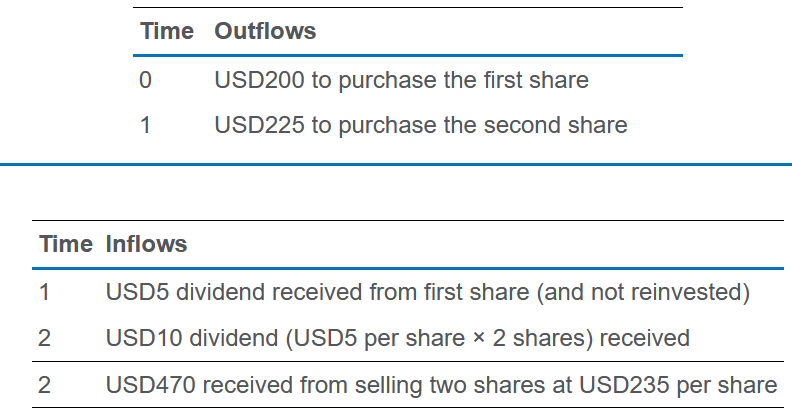
alt text

第一年的持有收益率是 $ (5+225-200)/200 = 15\% $

第二年的持有收益率是 $ \frac{(5\times 2+235\times 2-\boldsymbol{225}\times 2)}{\boldsymbol{225}\times 2} \approx 6.67\% $

然后就是第三步： $ (1+时间加权年回报率)^2 = (1+15\%)(1+6.67\%) $

年化收益率

$$ PV = FV_N(1+\frac{R_s}{m})^{-mN} $$

quoted年利率 $ R_s $，每年m个复利周期，一共N年。

对于不常见的利率，比如15日0.4%，就这样算：$(1+0.4\%)^{365/15}-1=10.02\%$

比如18个月20%，次方数是一年的12个月除以18个月：$(1+20\%)^{2/3}-1$

局限性：这样年化是假设能够每次都投到相同的利率；特别是对于短周期的的来说，不一定能做到。

continuously compounded return：

$$ FV = PV\times e^{rN} $$
$$ r_{t,t+1} = ln(P_{t+1}/P_t) = ln(1 + R_{t,t+1}) $$

比如一个星期的持有收益率是4%，那么所谓“一周连续复利回报率”就是$ln(1.04)$。根据简单的数学推理可知：

$$ r_{0,T}=r_{0,1}+...+r_{T-2,T-1}+r_{T-1,T} $$

其他

gross return：没有扣除管理费、保管费、税和其他management and administration支出之前的收益；但是交易费是要扣的。

net return就是扣了这些management and administration支出之后的。到这里就是pre-tax nominal income。

再扣除any allowance for taxes on dividends, interest, and realized gains就是after-tax nominal return。1

real return：

$$ 1+\text{nominal return}=(1+\text{real return})(1+\text{inflation premium})\\ 1+\text{real return}=(1+\text{real risk-free rate})(1+\text{risk premium}) $$

比如税率是20%，pre-tax nominal收益率是3%，通胀率是2%，那么after-tax real return就是 $ \frac{(1+3\%\times(1-20\%))}{1+2\%}-1=0.39\% $

杠杆收益率：Rp是产品收益率，VE是自己的钱，VB是借来的钱，rD是借来的钱的利率

$$ R_L=\frac{R_P\times(V_E+V_B)-V_B\times r_D}{V_E} \\=R_p+\frac{V_B}{V_E}(R_P-r_D) $$

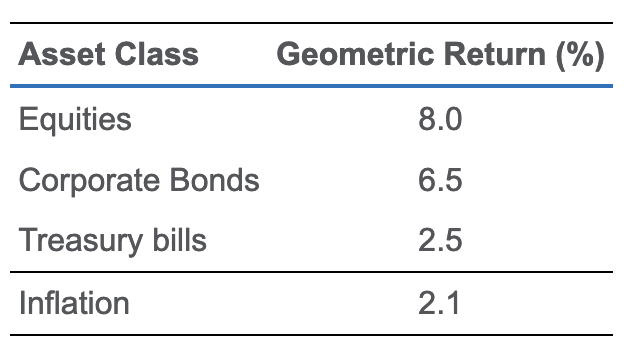
注意⚠️：如下图，如果要算risk premium，那就不用管inflation premium，因为所有的资产都面临相同的通胀premium，直接用$ \frac{1+\text{nominal return}}{1+\text{nominal risk-free return}}-1 $来算。

image-20240416195251574

货币时间价值（固定收益和权益）

Yield-to-maturity：the rate of return on a bond or loan

固定收益资产的现金流有三种类型：

  1. discount，支付一个PV，在到期时获得一个FV
  2. 定期利息：支付一个PV，固定间隔获得利息（PMT），到期时获得利息（PMT）和本金
  3. Level Payments：支付一个PV，固定间隔获得A（同时包含本金和利息）

Discount

$$ PV = FV_t/(1+r)^t $$

也叫 zero-coupon bond 。

定期利息

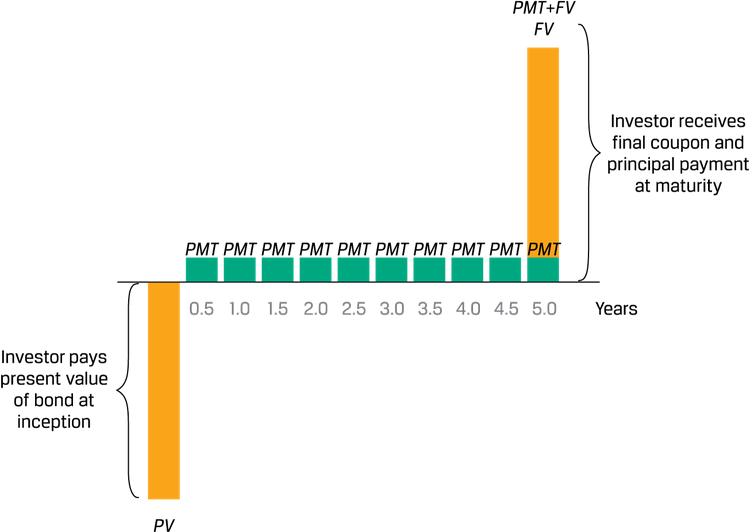
alt text

$$ PV = PMT_1/(1+r)^1+PMT_2/(1+r)^2+...+(PMT_N+FV_N)/(1+r)^N $$

永续债perpetual：

$$ PV=PMT/r $$

年金 Annuity

$$ A=\frac{r(PV)}{1-(1+r)^{-t}} $$

比如计算房贷，PV就是现在要贷的钱。用计算器的话，PV就是现在要贷的钱，N是Payment总次数（比如月供，30年，就是360），I/Y直接输年利率，FV是0；需要设置P/Y是12。

principal amortization and interest breakdown：

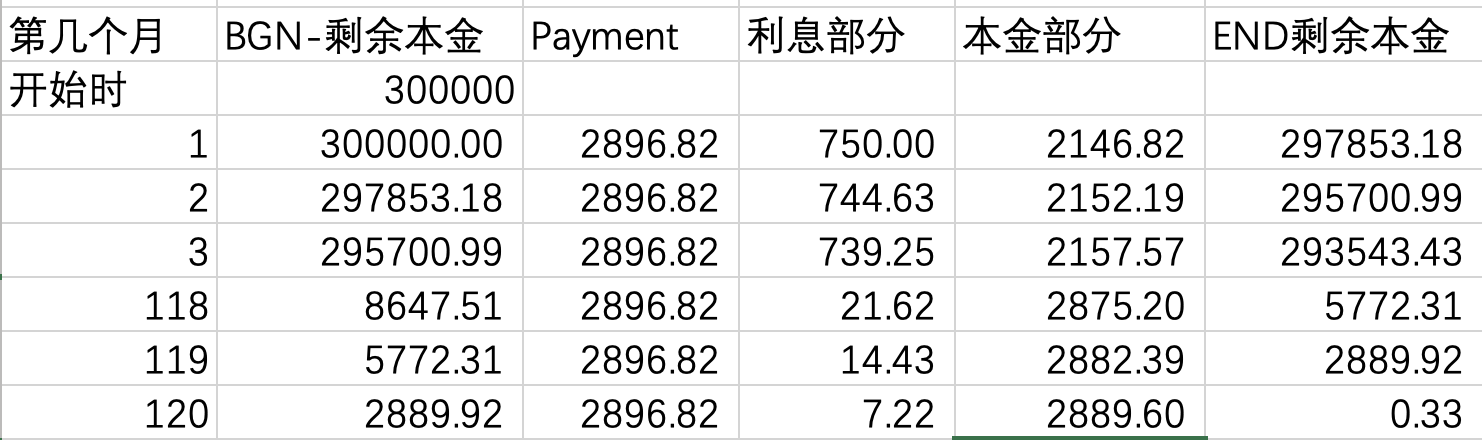
第一个月的利息是principal×利率（月利率）；principal amortization是算出来的PMT减去利息；然后用principal-principal amortization算剩余本金。第二个月的利息是剩余本金×利率，其他同上。所以Monthly Principal Repayment会越来越多，利息则越来越少。

比如10年，PV=30万，利率3%。用计算器可以得到PMT=2895.82。那么前几期和最后几期的：

alt text

equity

现金流有三种：

  1. 固定分红，支付PV之后获得固定的periodic分红（D）
  2. 固定增长率分红：支付PV之后，第一期的分红是 $ D_{t+1} $ ，然后分红以固定增长率g增长
  3. 可变增长率分红：支付PV之后，第一期的分红是 $ D_{t+1} $ ，但是后续的增长率不固定

固定分红的情况下跟perpetual一样， $ PV=D/r $

固定增长率的情况， $ PV=\frac{D_t(1+g)}{r-g}, \text{with } r-g >0 $​

可变增长率的情况，假设是两段式：

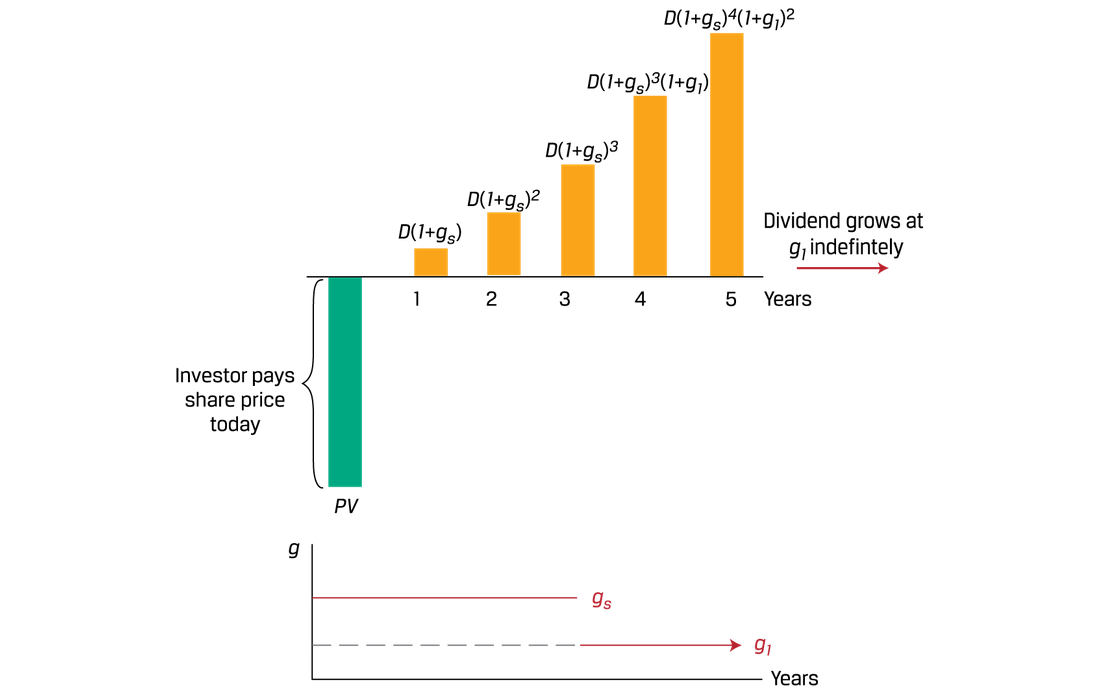
image-20240416231742892

$$ PV=\Sigma^n_{i=1}\frac{D_t(1+g_s)^i}{(1+r)^i}+\Sigma_{j=n+1}^\infty \frac{D_{t+n}(1+g_l)^j}{(1+r)^j}\\ =\Sigma^n_{i=1}\frac{D_t(1+g_s)^i}{(1+r)^i}+\frac{E(S_{t+n})}{(1+r)^n}\\ E(S_{t+n})=\frac{D_{t+n+1}}{r-g_l} $$

注意，两段式的第二段（增长率较低的那一段）的折现倍率是n；所以如果1到3年高增长，第4年开始低增长，是：

$$ PV=\Sigma_{i=1}^3\frac{D_t(1+g_H)^i}{(1+r)^i}+\frac{D_{3}(1+g_L)/(r-g_L)}{(1+r)^3} $$

隐含收益率和增长率

固定收益资产

固定收益资产的YTM就是隐含收益率。

discount的隐含收益率是

$$ r = \sqrt[t]{FV_t/PV}-1 $$

直接使用计算器的CF和I/Y都是不对的： alt text 需要先算出利息的FV，然后加到93.091上，然后再算出这个值的PV：

  1. N=2，I/Y=2，PV=0, PMT=2, 算FV=4.04
  2. 4.04+93.091=97.131，FV=93.171，PV=-100，PMT=0，算I/Y=-1.4449

注意这个题不是算后五年的YTM，而是算这两年的收益率，那么：

$$ FV_2 = PMT_1(1+r)+PMT_2+PV_2 r = \sqrt[2]{FV_2/PV}-1 $$

Equity

固定增长率：

$$ PV=\frac{D_t(1+g)}{r-g}\\ r = \frac{D_t(1+g)}{PV}+g $$

隐含增长率：

$$ PV=\frac{D_t(1+g)}{r-g}\\ g = r-\frac{D_{t+1}}{PV_t} $$
$$ P/E(\text{price to earnings per share})=\frac{Price}{\text{Earnings per share}} $$
$$ PV_t=\frac{D_t(1+g)}{r-g}\\ \frac{PV_t}{E_t}=\frac{\frac{D_t}{E_t}(1+g)}{r-g} $$

$ \frac{D_t}{E} $ 叫做dividend payout ratio。使用预测的下一期earnings per share，可以简化为：

$$ \frac{PV_t}{E_{t+1}}=\frac{\frac{D_{t+1}}{E_{t+1}}}{r-g} $$

cash flow additivity principle

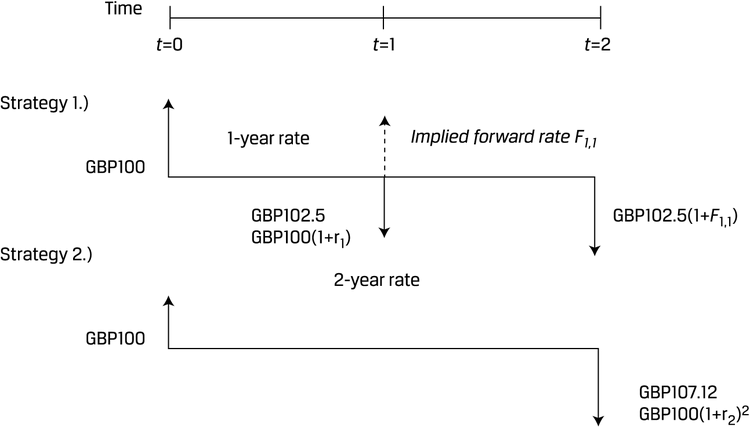
image-20240417105522030

IFR

Implied Forward Rate的算法是：

$$ FV_2 = FV_1\\ PV_0\times(1+r_2)^2 = PV_0\times(1+r_1)(1+IFR_{1,1}) $$

forward interest rate也可以称作breakeven one-year reinvestment rate in one year’s time。

如果给出PV，就要先算r再算forward interest rate： alt text 以计算2022年5月31日的1y1y IFR为例：

  1. 用计算器分别计算1y和2y的收益率
    1. N=1, PV=-98.028, PMT=0, FV=100, 计算I/Y=2.011670%
    2. N=2, PV=-95.109, PMT=0, FV=100, 计算I/Y=2.529027%
  2. 应用公式 $ (1+r_1)(1+IFR{1,1})=(1+r_2)^2 $ 算出IFR

同理可确定不同货币的forward exchange rate，不过要注意使用连续复利（e）。

alt text

期权定价

  1. t=0时标的是40元；=1时有可能是56，有可能是32；求期权价格c0

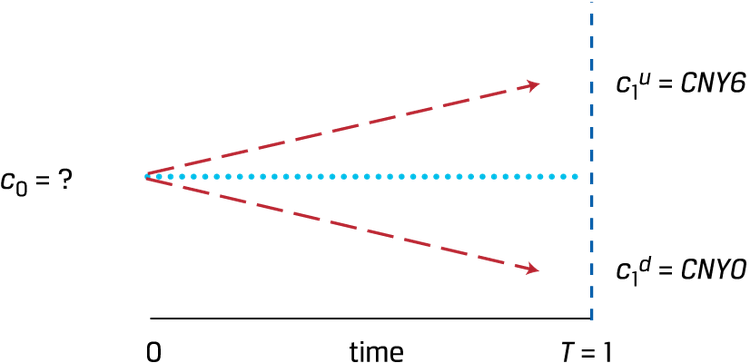
alt text

首先要构造一个portfolio使得t=1时无论哪种情况现金流都一样。这里需要算的是购买多少unit的标的：

$$ V_0=x\times 40 - c_0\\ V_1^u = x \times 56 - 6\\ V_1^d = x \times 32 - 0\\ V_1^u = V_1^d \\ x\times 56-6=x\times 32-0 $$

算出x之后可以得到t=1时的现金流，就可以算t=0时的c0了：

$$ x = 0.25\\ V_0=0.25\times 40 - c_0 = \frac{V_1^d}{1+r} $$

其中x又叫做hedge ratio。

分位数算法

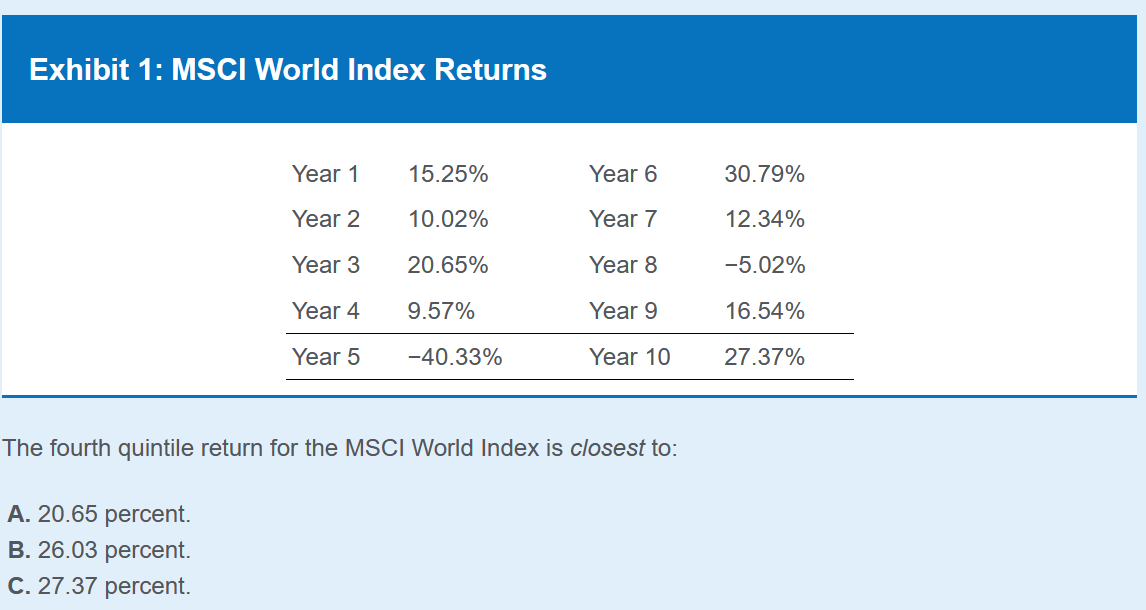
alt text

$$ L_y = (n+1)\times(y/100) $$

所以第4个5分位就是：

$$ L_{80} = (10+1)\times(80/100)=8.8\\ \text{由低到高排列之后，第8位是20.65，剩下的0.8用线性插值：}\\ P_{80} = 20.65+0.8\times (27.37-20.65) $$

Coefficient of Variation

简称CV， $ CV=\frac{s}{\bar X} $ 。CV越大越风险。

偏度峰度

Skewness偏度，正偏度指frequent small losses和a few extreme gains；负偏度反过来：

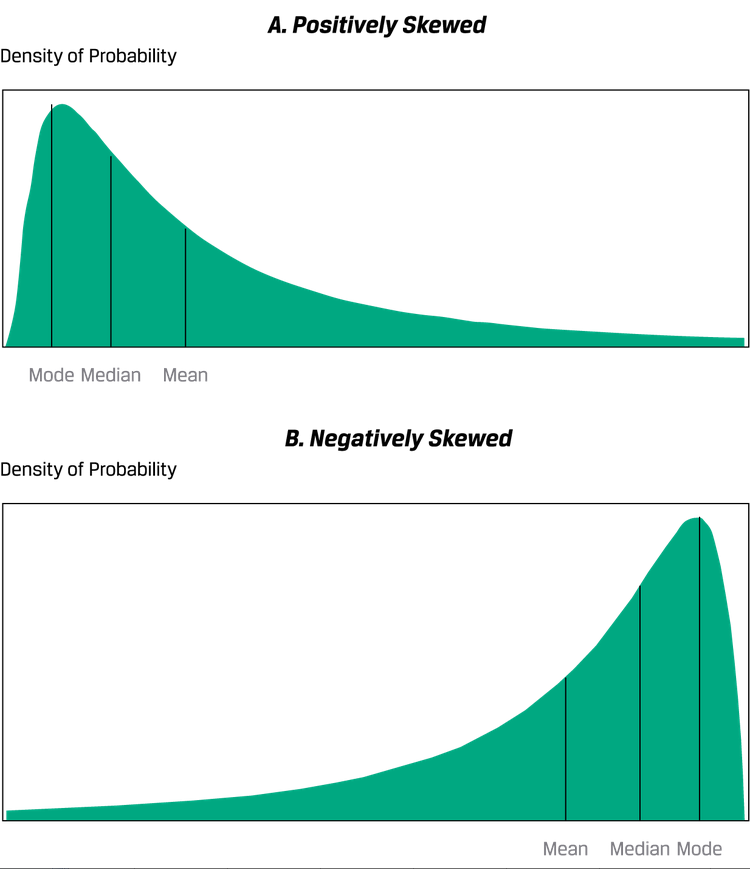
alt text

投资者通常会被正偏度吸引，因为平均数比中位数大。

$$ \text{Skewness} \approx (\frac{1}{n})\frac{\Sigma_{i=1}^n{(X_i-\bar X)}^3}{s^3} $$

峰度：xx个标准差之外的总probability的占比。

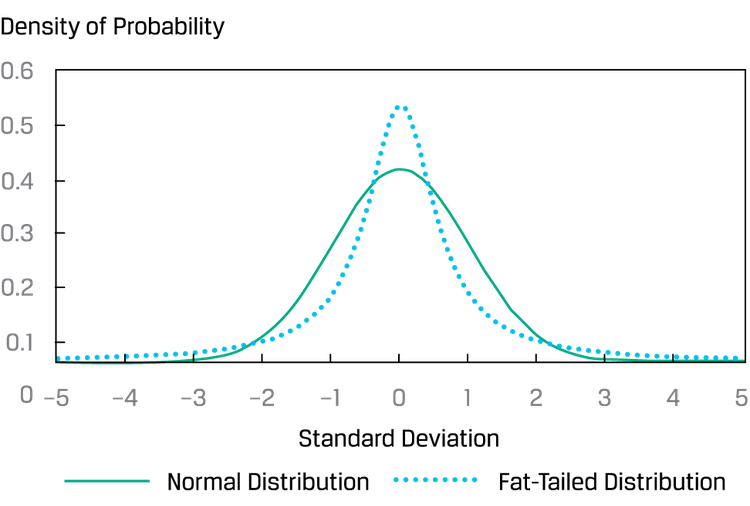
alt text

fat-tail 对应的是 leptokurtic（尖峰）；thin-tail对应的是platykurtic（平峰）；标准正态的是msokurtic（峰度3）。fat-tail可以理解为风险更高。

通常会计算excess kurtosis（与标准正态的3对比）；对于样本大于100的：

$$ K_E \approx (\frac{1}{n})\frac{\Sigma_{i=1}^n{(X_i-\bar X)}^4}{s^4}-3 $$

Correlation

Sample covariance：

$$ s_{XY} = \frac{\Sigma_{i=1}^n{(X_i-\bar X)(Y_i-\bar Y)}}{n-1} $$

如果X大于平均值时Y也大于平均值，X小于平均值时Y也小于平均值，那么covariance就会是正的。

sample correlation coefficient，去掉了单位：

$$ r_{XY}=\frac{s_{XY}}{s_X s_Y} $$

会显示线性相关的强度：

  • $ -1 \le r_{XY} \le 1 $
  • 0代表没有线性关系
  • 1代表强正线性相关；-1代表强负线性相关

注意，可能存在非线性相关，但是这个指标不能反映这个事实：

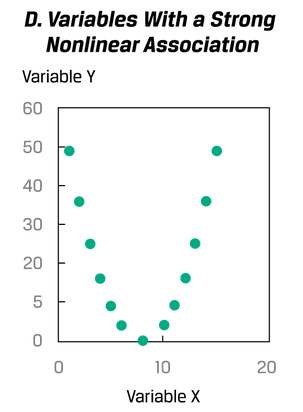
alt text

以及对极端值很敏感，需要考虑是否排除（用点阵图来预览）；相关不代表因果。

spurious correlation（虚假相关），有三种情况：

  • 只在特定数据集中存在
  • 计算时混入了第三个变量
  • 两个变量间的相关是来自于它们各自跟第三个变量的关系而不是direct2

相同的平均数、标准差和相关性不能够完全确定整个变量分布是怎么样的。

Expected

Expected的是forecast，是population。

$$ E(X)=\Sigma_1^n{P(X_i)X_i}, \text{ P是概率}\\ \sigma^2(X)=\Sigma_1^n{P(X_i)(X_i-E(X))^2} $$

用计算器：DATA，X输入X，Y输入概率（百分数，不能输小数形式）

Conditional

alt text

从右向左计算，无论是conditional expected还是conditional variance。

贝叶斯公式 Bayes’ Formula

贝叶斯公式是用来在获得新信息的时候调整已有的结论的方法。

$$ P(\text{Event|Information}) = \frac{P(\text{Information|Event})}{P(\text{Information})}P(\text{Event}) $$

更新后的概率叫做posterior probability。

如果 prior probabilities 都相等，就叫做diffuse priors，那么事件的概率就完全由信息决定。

Portfolio Expected

expected return on the portfolio：加权平均回报率：

$$ E(R_p)=w_1E(R_1)+w_2E(R_2)+...+w_nE(R_n) $$

Covariance的公式是（没什么用，看看就行）：

$$ Cov(R_i,R_j)=E[(R_i-ER_i)(R_j-ER_j)] $$

Portfolio variance（也没什么用，看看就行）：

$$ \sigma^2(R_p)=E[(R_p−ER_p)^2]=\Sigma^n_{i=1}\Sigma^n_{j=1}{w_iw_jCov(R_i,R_j)} $$

假设给出以下信息，则可以开算：

alt text

Covariance Matrix: 注意图里面的数字的单位都是%的平方；比如400是指0.04；在练习中问covariance的时候也是回答400而不是0.04。

alt text

$$ \sigma^2(R_p)=w_1^2\sigma^2(R_1)+w_2^2\sigma^2(R_2)+w_3^2\sigma^2(R_3)\\+2w_1w_2Cov(R_1,R_2)+2w_1w_3Cov(R_1,R_3)+2w_2w_3Cov(R_2,R_3)\\ =0.50^2\times 400+0.25^2\times 80+0.25^2\times 441+2\times 0.5 \times 0.25 \times 45 +... $$

资产分散带来的风险降低：如果portfolio的构成都是independent的，cov就会都是0，那portfolio variance比起非independent时会更小；如果是负相关的，cov小于0，variance更小。

Correlation：

$$ \rho(R_i,R_j)=\frac{Cov(R_i,R_j)}{\sigma(R_i)\sigma(R_j)} $$

用Covariance Matrix可以直接得出Correlation Matrix。与前面的相同，上下限是 $ [-1,1] $，绝对值越接近1就越线性相关。

Joint Probability Function

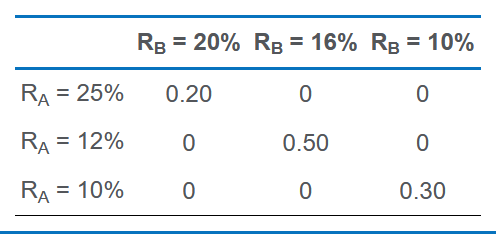
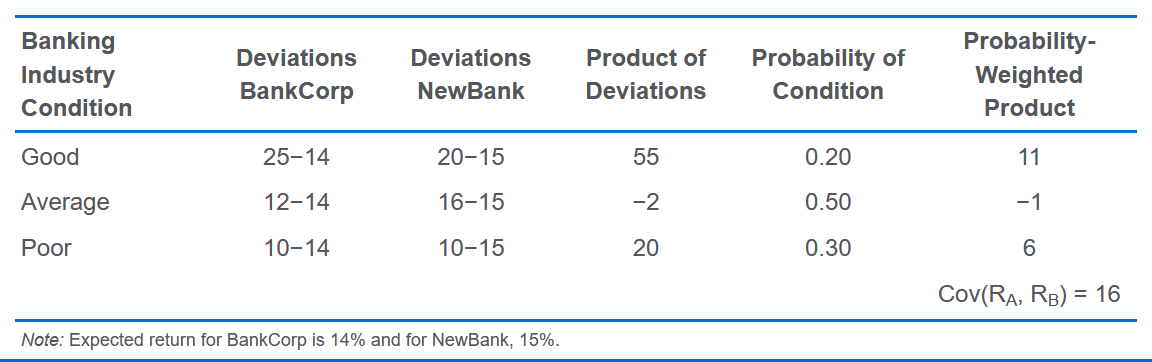
alt text

根据这个表可以算出A的平均回报是 $ 0.2\times 25\% + 0.5 \times 12\% + 0.3 \times 10\% = 14\% $，B同理得15%。然后构造下表，解释第一行：

  • Good对应第一个表的25%和20%
  • 先算两个与平均值的差，25-14是25%减平均值14%
  • 将两个差相乘，再乘以权重0.2

算出所有情况之后加起来就是Cov。

alt text

独立

如果两个变量独立，那么 $ P(XY)=P(X)P(Y) $

如果两个变量uncorrelated，那么 $ E(XY)=E(X)E(Y) $

mean–variance analysis

有三个假设：

  1. 风险厌恶
  2. 最大化预期utility或satisfaction
  3. 或：
    1. 回报是正态分布的
    2. 投资者的效用方程是二次的

如果都满足，那么就是exactly；如果第三条不满足，就是approximately。

如果只考虑downward risk（shortfall risk），可以用safety-first rules。

最低可接受收益是 $ R_L $，那么投资者的目的就是选择 $ P(R_p<R_L) $ 最小的那个组合；return是正态分布的情况下，相当于选出一个最大的：

$$ \text{SFRatio} = [E(R_P) − R_L]/σ_P $$

每个投资组合return低于 $ R_L $ 的概率是 $ NORM(-\text{SFRatio}) $ 。当 $ R_L = R_{\text{risk free}} $ 的时候，就成了夏普比率。

value at risk （VaR）：特定时间内、特定可能性下，可能损失的最小金额。比如95 percent one-day VaR就是一天内有0.05的可能损失至少这个金额。

Stress testing and scenario analysis refer to a set of techniques for estimating losses in extremely unfavorable combinations of events or scenarios。

Lognormal 对数正态分布

偏度是正的，右尾很长。

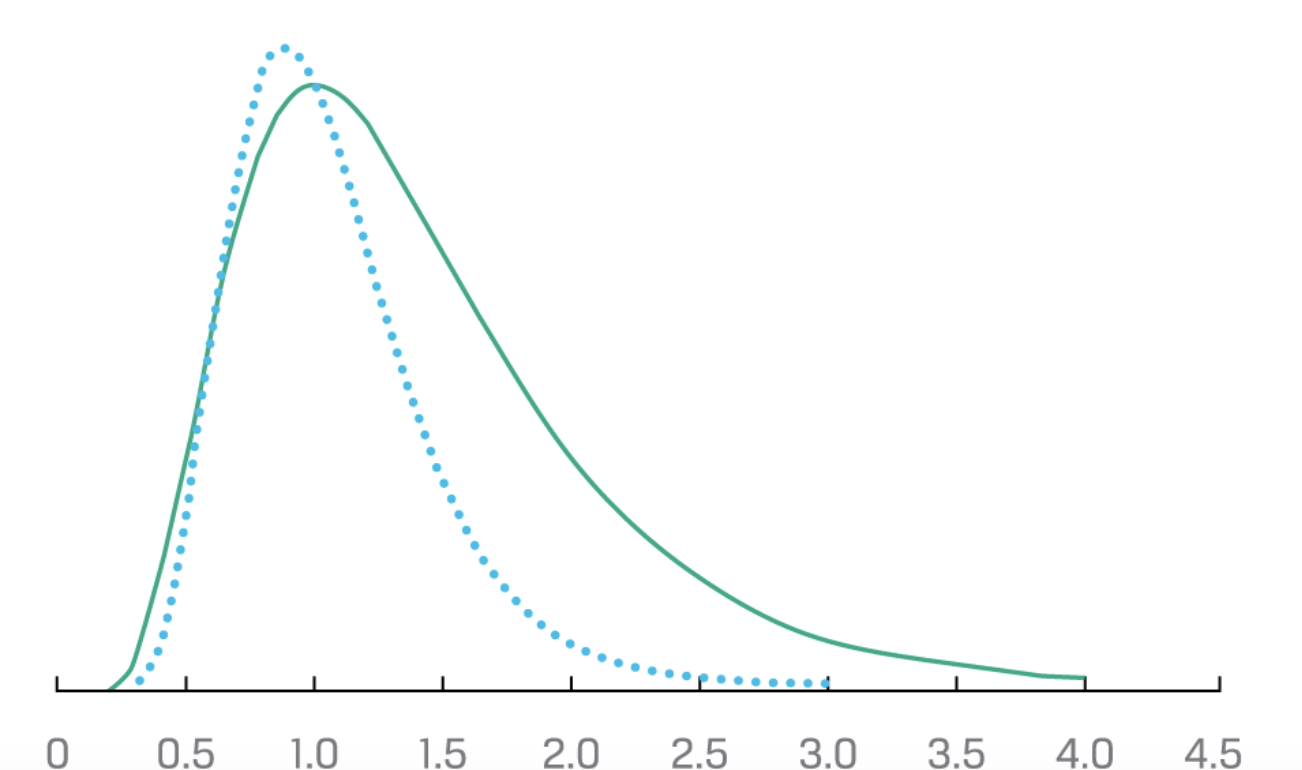
Alt text

$$ \text{Mean} = e^{\mu+0.5\sigma^2}\\ \text{Variance} = e^{2\mu+\sigma^2}\times e^{\sigma^2-1} $$
  1. 如果continuously compounded return是正态分布的，那么未来的股价必定lognormal
  2. 即使continuously compounded return不是正态分布，如果满足中心极限定理，那未来股价也可以lognormal。
$$ \text{因为} P_T=P_0\times e^{r_{0,T}}\\ \text{又有} r_{0,T} = r_{0,1}+r_{1,2}+...+r_{T-1,T}\\ \text{所以如果} r_{0,T} \text{是正态分布的，那么} P_T \text{是lognormal的} $$

i.i.d：回报率是independently and identically distributed；independence导致不能用过去的returns预测未来return；identical导致平均数和方差不变。从而有：

$$ E(r_{0,T}) = \mu T \\ \sigma^2(r_{0,T}) = \sigma^2 T $$

这是continuously compounded return的正态分布的参数，可以用来算股价（lognormal）的参数。

volatility是continuously compounded returns的standard deviation

给定daily volatility假设为0.01，那么年的volatility就是 $ 0.01\times \sqrt{250} $ 。通常的计算过程：获取日持有收益率，转换为continuously compounded daily returns，然后计算标准差（即daily volatility）：

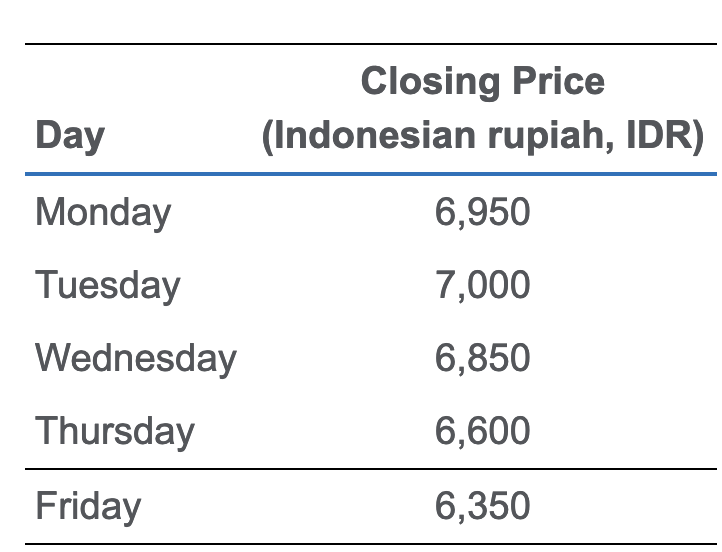
Alt text

计算器用STAT的1-V，但是DATA需要自己转换成ln；1-V算出来的是daily，需要转换成年（ $ E(r_{0,T}) = \mu T $ ）。

$$ X01 = ln(7000/6950) $$

蒙特卡洛模拟和bootstrap模拟

没时间记了。

bootstrap是抽了还放回去，jackknife是抽了不放回去。

Sampling method

probability sampling：pop里面每个element都有相同的机会被选中

non-prob samp：sampler’s judgment or the convenience to access data会影响概率。

Prob

简单随机抽样。系统抽样（每k个抽一个）。

抽样就会有sampling error。统计量也是随机变量，存在分布。统计量的抽样分布是统计量在从同一总体中随机抽取的相同大小的样本计算时可以假设的所有不同可能值的分布。

Stratified Random Sampling分层随机抽样。先把population分组，然后 $ \frac{每组样本数}{总样本数} = \frac{每组大小}{pop大小} $ 。

Cluster抽样，将pop分成小cluster，每个cluster其实都是pop的一个缩影；以cluster为单位进行简单随机抽样。one-stage是选中的cluster的所有member都作为样本；two-stage是选中的cluster再抽sub-sample。

Non-prob

方便抽样（Convenience Sampling）。

Judgmental Sampling。based on a researcher’s knowledge and professional judgment

中心极限定理及相关

只要样本量够大，那么分布就会近似正态，参数是 $ \mu $ 和 $ \sigma^2/n $ 。

the standard error of the statistic指sample statistic的标准差。

sample mean的standard error就是 $ \sigma_{\bar X} = \frac{\sigma}{\sqrt{n}} \text{或} s_{\bar X} = \frac{s}{\sqrt{n}} $ 。

实践中很难知道pop的方差，所以都会用样本方差：

$$ s^2=\frac{\Sigma{(X_i-\bar X)^2}}{n-1} $$

总而言之，中心极限定理说的是，只要样本量够大：

  1. $ \bar X $ 的分布近似正态
  2. $ \bar X $ 的分布的均值等于pop的均值
  3. $ \bar X $ 的分布的方差等于pop的方差除以样本大小

Alt text

用1-V算 $ \sigma $ ，再除以 $ \sqrt{10-1} $ 。计算器算的s不是standard error，是sample standard deviation。

假设检验

总表：

Alt text

相关内容：笔记

independent samples（not paired）用difference in mean；

dependent samples（paired）用mean of differences。

Type I：H0是真的但是reject了；Type II：H0是假的但是没有reject。

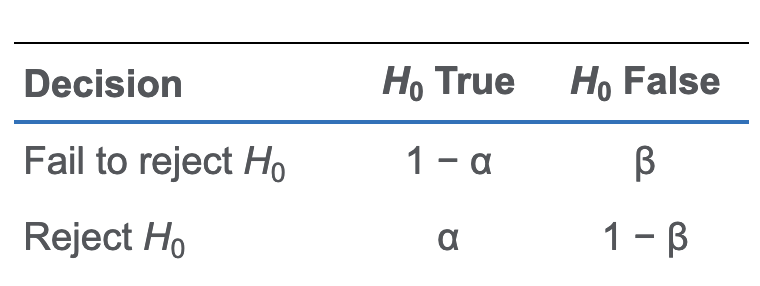
Alt text

Power of test是 $ 1- \beta $ 。

非参数检验

前一节的检验都有两个特征：1）检验的是parameter；2）有一些前提假设（比如正态分布）。

非参数检验有以下场景：

  1. data不满足分布要求
  2. 有极端值
  3. 是rank或者ordinal数据
  4. 不是parameter

独立性检验

Corr的参数检验也称Pearson correlation/bivariate correlation，是为了检验两个pop之间是否存在线性关系（correlation coefficient）。

基于 sample correlation 的公式 $ r = \frac{s_{XY}}{s_Xs_Y} $ ，如果X和Y都服从正态分布，则用t检验 $ H_0: \rho = 0 $ ：

$$ t= \frac{r\sqrt{n-2}}{\sqrt{1-r^2}} $$

自由度是n-2。样本量越大，reject所需的r越小；r越大，实现所需的显著性所需要的n越小。

非参数检验有Spearman rank correlation coefficient：

  1. 将sample X从大到小排列，最大设为1，第二是2，如此类推；如果两个数相等，那就设为平均值（比如第三和第四相等，那就都设置为3.5）；Y也是这样操作
  2. 计算每对值的rank差别 $ d_i $ （这里的每对是恢复了原来的排序的，所以存在差别）
$$ r_s=1-\frac{6\times\Sigma{d_i^2}}{n(n^2-1)} $$

示例：

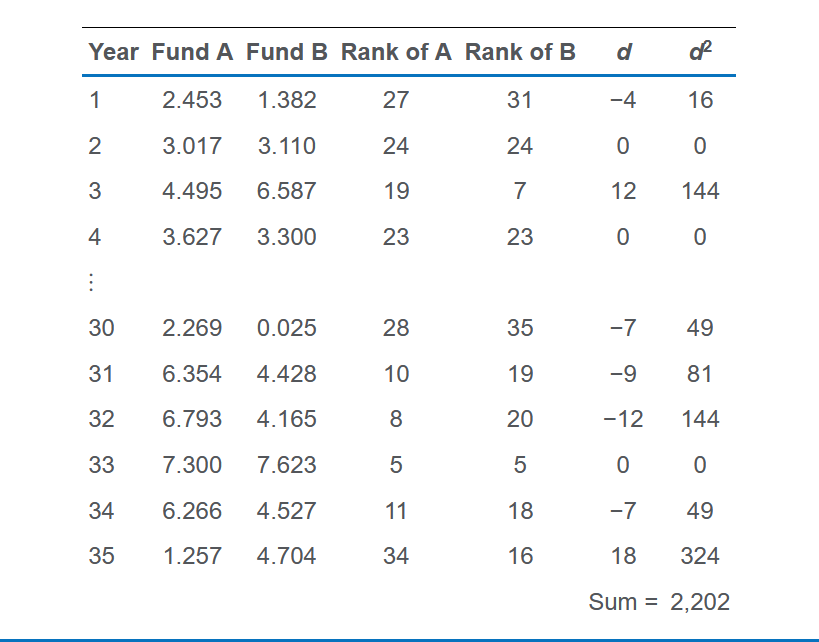
alt text

对于n大于30，就可以将 $ r_s $ 代入 $ t= \frac{r\sqrt{n-2}}{\sqrt{1-r^2}} $ 中做检验；否则需要一个特殊表格。

如果是categorical或者是离散数据，就没办法用前面两种方法来判断独立性。

$$ \chi ^2 = \Sigma_{i=1}^m{\frac{(O_{ij}-E_{ij})^2}{E_{ij}}} $$

结合示例来看：

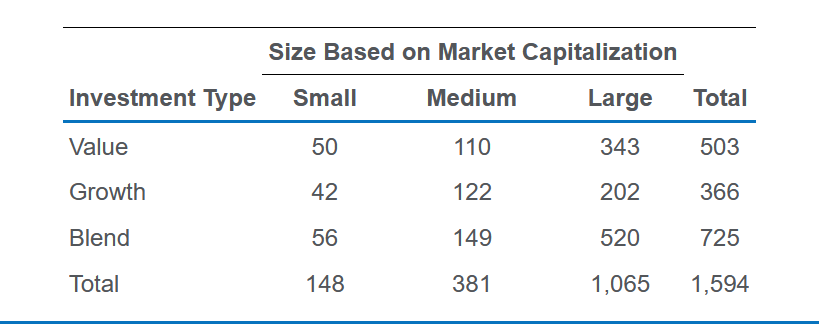
alt text

分类1有3种，分类2有3种，所以m=3×3=9； $ O_{ij} $ 是每个格子（sum的那些除外）的值； 一个 $ O_{ij} $ 对应的 $ E_{ij} $ 是这个格子的行sum乘以列sum除以总sum。例如small-cap value的 $ E_{ij} $ 是 $ \frac{503\times 148}{1594} = 46.703 $

算出来用卡方检验，自由度是 $ (n_1 - 1)(n_2 -1) = 2 \times 2 $ ，注意检验是单侧的。

（简单）线性回归

因变量Y的方差和叫做 sum of squares total (SST) 。

$$ Y_i = b_0 + b_1X_i+ \epsilon_i $$

b0是intercept，b1是slope coefficient，这俩叫做回归系数（regression coefficients）；$ \epsilon $ 是误差（error）。

注意， $ \epsilon $ 是sample和pop之间的；而 residual 是sample和当前line之间的。

$$ e_i = Y_i- \hat{Y}_i $$

目的是找到最小方差的那条线，所以又称ordinary least squares (OLS) regression；用 residual 来说就是最小化 $ \Sigma{e_i^2} $ ，sum of squares error (SSE)。 residual的单位与Y相同。

计算（都用计算器算，这里随便看看）：斜率系数是X,Y的covariance除以X的variance：

$$ \hat{b}_1 = \frac{\frac{\Sigma{(Y_i-\bar Y)(X_i-\bar X)}}{n-1}}{\frac{\Sigma{(X_i-\bar X)^2}}{n-1}}\\ =\frac{\Sigma{(Y_i-\bar Y)(X_i-\bar X)}}{\Sigma{(X_i-\bar X)^2}} $$
$$ \hat{b}_0=\bar Y- \hat{b}_1 \bar X $$

需要满足的前提：

  1. 线性关系
  2. 同方差（Homoskedasticity）：对于所有observations，residual的方差相同
  3. XY互相独立
  4. residual是正态分布（或者是大样本）

sample covariance就是X,Y的协方差除以n-1：

$$ \frac{\Sigma{(X_i-\bar X)(Y_i-\bar Y)}}{n-1} $$

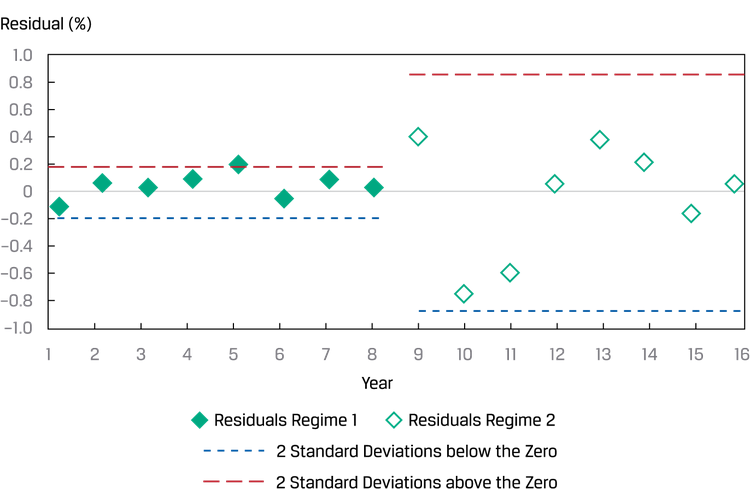
X不能是random的，但是residual最好是random的；如果residual跟X看起来存在关系，则可能XY不是线性关系，或者XY不是互相独立：

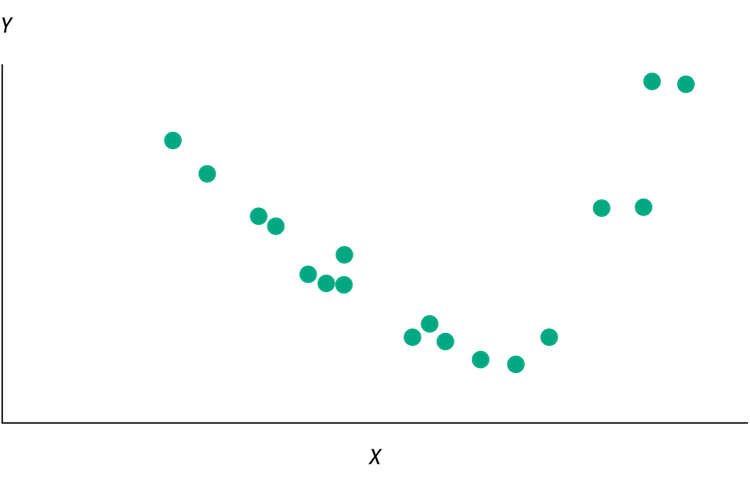
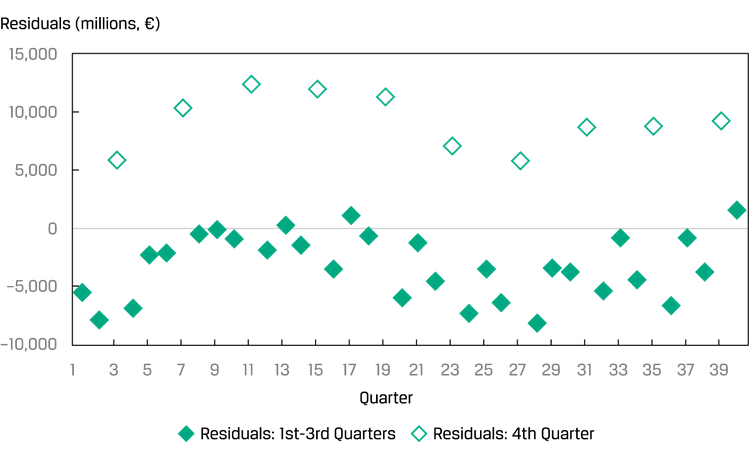
alt text

alt text

不满足前提2的举例：Y是利率，X是通胀率，中央银行在中间的某个节点进行了干预控制利率，就会导致方差不同：

alt text

模型效果检验 Goodness of Fit

sum of squares regression（SSR）：

$$ \text{SSR} = \Sigma{(\hat{Y}_i-\bar Y)^2}\\ \text{SSE} = \Sigma{(Y_i- \hat{Y}_i)^2}\\ \text{SST} = \text{SSR}+\text{SSE} $$

SSR是explained variation，所以是hat - bar；SSE是unexplained variation。

coefficient of determination（ $ R^2 $ ）：

$R^2 = \frac{\text{SSR}}{\text{SST}}$ alt text

在计算器中，线性回归的r的平方就是 $ R^2 $ 。

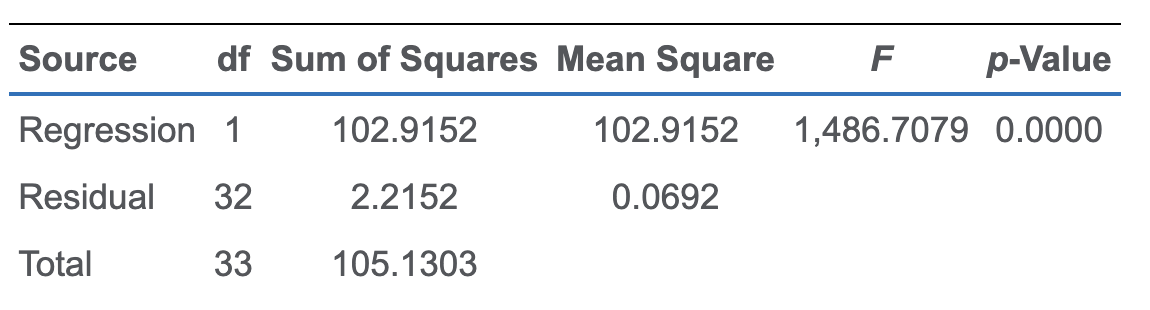
$ R^2 $ 是描述性的，如果要检验统计上有意义，就要做F检验。

null和alt：

$$ H_0: b_1 = 0\\ H_a: b_1 ≠ 0 $$

F检验的值是SSR和SSE各自根据自由度调整之后相除；SSR除以自由度叫做mean square regression (MSR)；SSE除以自由度叫做mean square error (MSE)

MSR的自由度是X的个数k，这里是1；MSE的自由度是n-k-1，这里是n-2。

$s_e = \sqrt{MSE}\\ MSE=SSE/(n-k-1)\\ MSR=SSR/(k)$ alt text

$$ F=\frac{\frac{SSR}{k}}{\frac{SSE}{n-k-1}}=\frac{\Sigma{(\hat{Y}_i-\bar Y)^2}}{\frac{\Sigma{(Y_i- \hat{Y}_i)^2}}{n-2}} $$

这个F检验是单侧的，reject区域在右侧——希望explained的比unexplained的多。

斜率系数检验

比如想要检验一个股票是否是平均系统性风险。相当于检验single mean，用t检验。

有一个假设的pop的斜率 $ B_1 $ ，t检验值：

$$ t= \frac{\hat{b}_1-B_1}{s_{\hat{b}_1}}, \text{自由度n-2} $$

$ s_{\hat{b}_1} $ 是standard error of the slope coefficient（斜率系数的标准差），是 model’s standard error of the estimate （ $ s_e $ ）除以X的标准差：

$$ s_{\hat{b}_1}=\frac{s_e}{\sqrt{\Sigma{(X_i-\bar X)^2}}} \\ s_e=\sqrt{\text{MSE}} $$

特点

检验斜率是否为0的t检验的值等于检验XY的corr的t检验。也就是说以下两个是等价的：

  • $ H_0: \hat{b}_1 = 0 $
  • $ H_0: \rho = 0 $
  • 只要等号、不等号的方向相同、数字相同，这两个就是等价的

所以用计算器的r带入 $ t= \frac{r\sqrt{n-2}}{\sqrt{1-r^2}} $。

同时，检验斜率是否为0的 t 的平方等于检验 拟合度的F值。

截距检验

$$ s_{\hat{b}_0}={s_e}\sqrt{\frac{1}{n}+\frac{\bar{X}^2}{\Sigma{(X_i-\bar X)^2}}} $$
$$ t = \frac{\hat{b}_0 - B_0}{s_{\hat{b}_0}} $$

indicator variable（发生了事件就1，否则是0的变量）的假设检验是相同的。

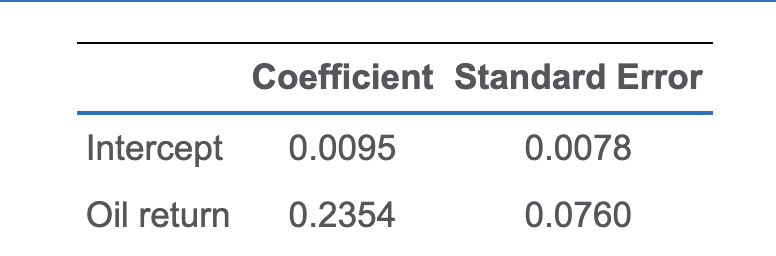
例题

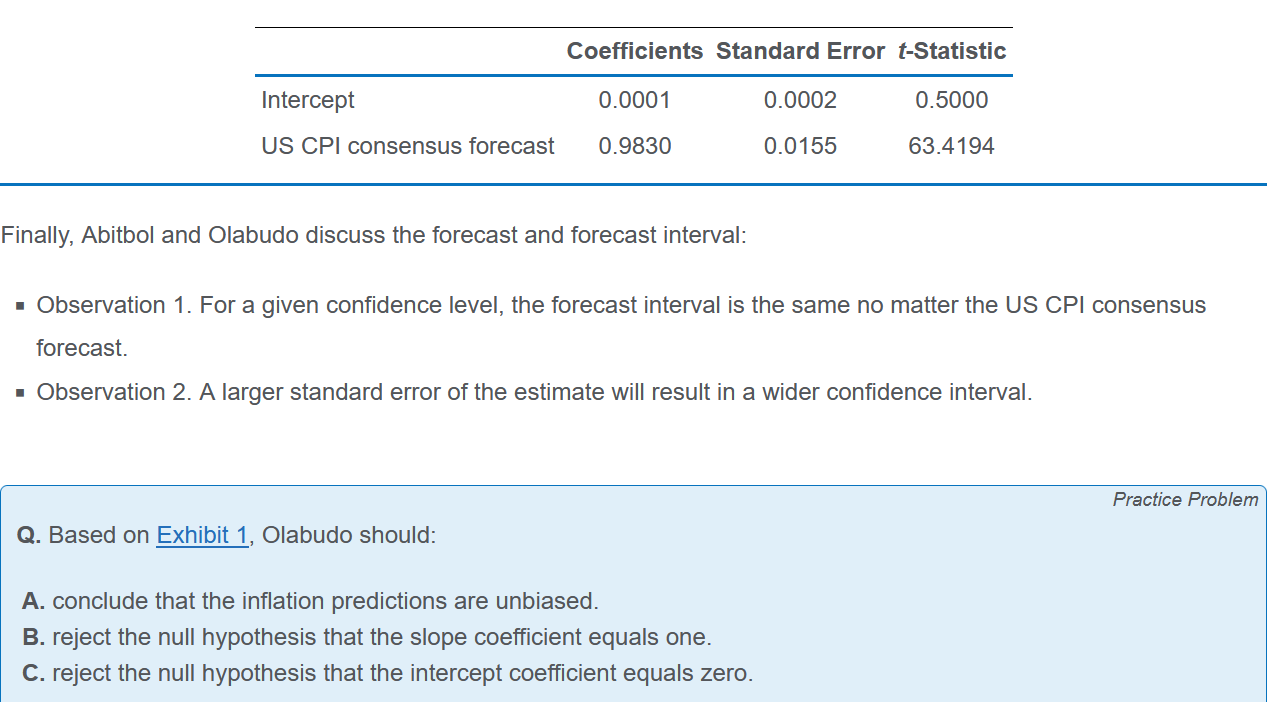
alt text

alt text

此处使用的是 $ t=\frac{\hat{b_1}-B_1}{s_{\hat b}} $：

  1. $ \hat{b_1} $ =0.9830， $ B_1 $ = 1
  2. $ s_{\hat b} $ 就是途中第二行的standard error

检验基本上都是coefficient减去目标值除以standard error： alt text alt text

p值

p值是拒绝null的最小的显著性水平。如果p=0.005而显著性是0.5时，就可以拒绝。显著性是percent，0.5%等于0.005

ANOVA

analysis of variance表格：

alt text

Y的方差是SSE除以n-1。

standard error of the estimate（ $ s_e $ ）就是MSE开根号；越小，模型越fit。

F和 $ R^2 $ 都是relative的，而 $ s_e $ 是绝对的。

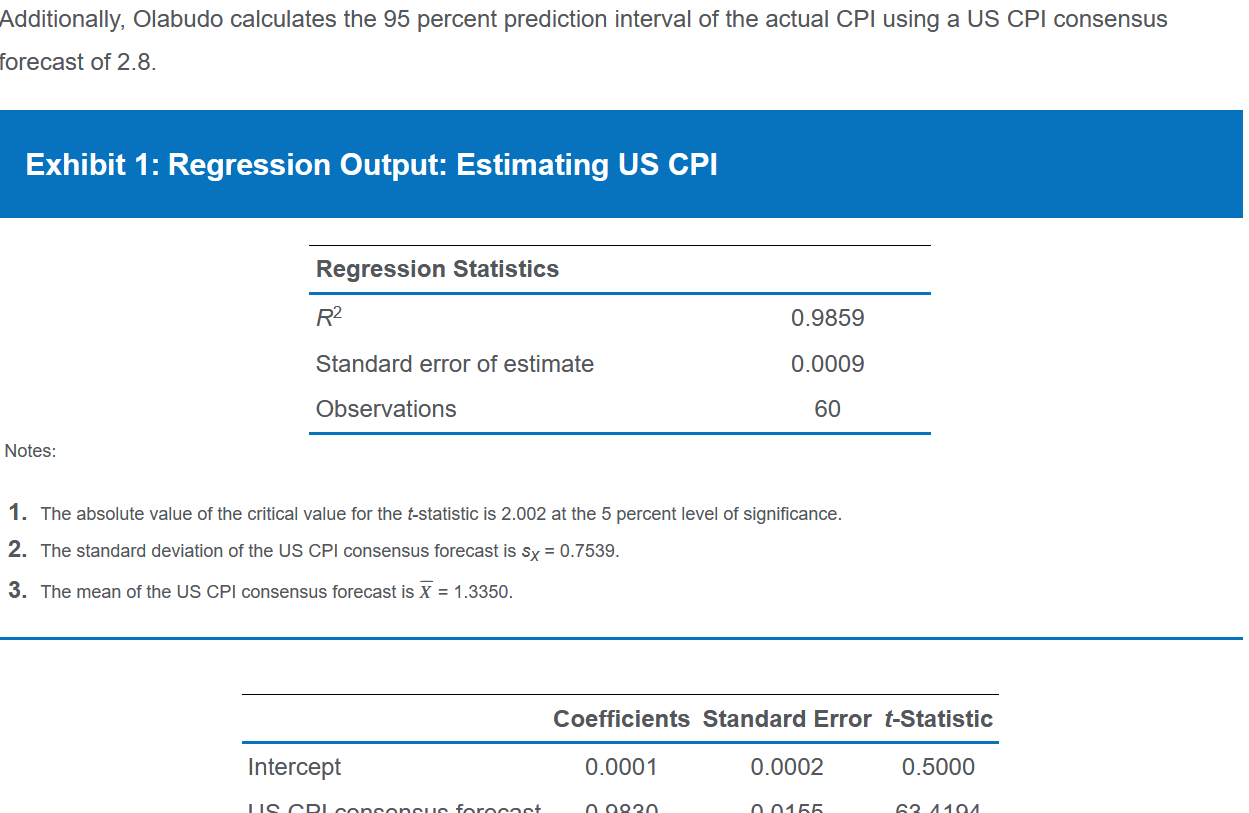
prediction

$$ \hat{Y}_f = \hat{b}_0+\hat{b}_1X_f $$

预测会存在方差：

$$ s_f^2 = s_e^2[1+\frac{1}{n}+\frac{(X_f−\bar X)^2}{\Sigma{(X_i−\bar X)^2}}]\\ s_f^2 = s_e^2[1+\frac{1}{n}+\frac{(X_f−\bar X)^2}{(n-1)s_X^2}] $$

预测的X与均值相差越小，方差就越小；样本量越大，方差越小；拟合越好，方差越小。

得到标准差之后就可以得到预测区间（interval）：

$$ \hat{Y_f}±(t_{\alpha/2}\times s_f) $$

alt text

线性回归参数转换

  1. log-lin（ln Y，X）
  2. lin-log
  3. log-log

log了就变成relative change了。log-lin和lin-lin不能直接对比，因为Y的单位不同了；相反，lin-log可以和lin-lin对比。

选择哪种，需要对比 $ R^2 $ 、 F检验以及 $ s_e $ ；最关键的是residual是否表现出pattern——目的是residual是random的。

Fintech

与投资相关的fintech部分：analysis of large datasets；analytical tools比如AI。

Big data的特征：volume大；velocity（产生速度）快；variety多。用于预测时，还有一个veracity：the credibility and reliability of different data sources。

Big data来源：金融市场、商业、政府、个人、传感器、IoT（物联网）。

Alternate data的主要来源：个人、商业过程、传感器。

ML algorithms aim to “find the pattern, apply the pattern.”

ML需要将dataset分成三个：training、validation、test。最大的限制是需要大量的数据来训练。需要留意overfitting和underfit，一个是把noise当真了，一个是把真的当noise了。

ML通常分三类：

  1. 监管学习：根据标注了的训练数据寻找model
  2. 无监管学习：数据没有标注
  3. 深度学习（神经网络）

Data处理方法：

  • capture
  • curation（在清理过程中保持质量和准确性）
  • storage
  • search
  • transfer

对于文本这种非结构化数据，需要做文本分析（text analytics）。经典的包括自然语言处理（NLP）。

  1. Bonds issued at a discount to the par value may be taxed based on accrued gains instead of realized gains. ↩

  2. 第二类和第三类的区别举例：第二类：把X和Y分别除以Z，导致相关性增加；第三类：身高和词汇量相关性很强，但是是因为身高随年龄增加而增加、词汇量随年龄增加而增加。 ↩

目录