CFA笔记 Hypothesis Testing

于 2024-03-13 发布

Hypothesis testing：通过测试来确定一个sample statistic是不是来自于一个population with the hypothesized value of the population parameter。

flowchart TD
A["State the hypotheses"] --> B[Identify the appropiate test statistic]
B --> C[Specify the level of significance]
C --> D[State the decision rule]
D --> E[Collect data and calculate the test statistic]
E --> F[Make a decision]

State the Hypotheses

每个hypothesis testing都有两个假设：null hypothesis（$ H_0 $）和alternative hypothesis（$ H_a $）。null是默认为真的，除非通过testing证明不是真，那么就采用alternate。目标就是证明null不是真。两个假设都是以population parameter来进行假设的，然后用sample statistics来验证。

Two-sided和one-sided假设：以mean举例，如果是假设“是否等于某个值”，那么就是two-sided（因为既可以大于也可以小于）；如果假设“大于/小于等于”那就是单侧。

在金融中，one-side更加反映researcher的倾向性；而如果one-side也是reasonable的情况下采用了two-side，那就是想表达中立性。

常用Test Statistics

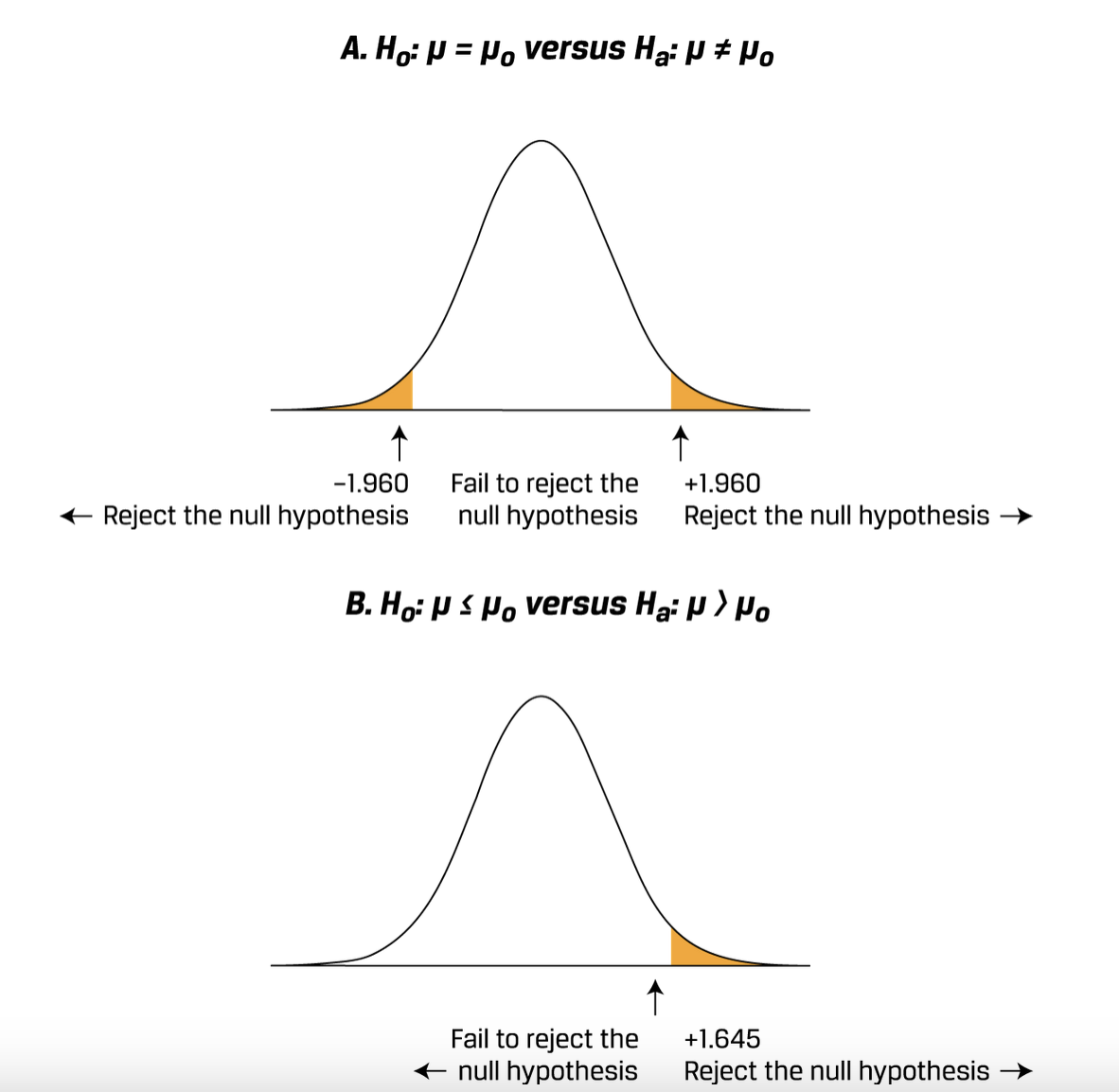
Alt text

Alt text

根据alternative来确定critical value是哪边：

  1. 不等于，就是两边
  2. 大于，就是右边
  3. 小于，就是左边

Test of a single mean

要求符合（t分布或z分布的）前提：population分布是正态或近似正态，或者样本量够大。

Test of difference in means

情景：想要知道两个样本的mean是否相同

前提：population是正态或近似正态，样本之间independent；（以及在这个讨论范围内假设population variance相同，合并使用两个样本来获得pooled estimate of the common population variance）

$$ t=\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{\sqrt{\frac{s_p^2}{n_1}+\frac{s_p^2}{n_2}}}, \\ \text{where }s_p^2=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2} $$

$ s_p^2 $ 实际上是两个样本的方差的加权平均数。

如果两个pop方差未知且不同：

$$ t=\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}} $$

alt text

Test of the mean of the differences

如果样本是dependent的，那么测试mean就不是前面的步骤了。比如测试税法变化前后的同一组公司的分红情况，比如测试相同底层资产的两种不同策略的收益情况。

前提：differences是正态分布。

$$ t=\frac{\bar d - \mu_{d0}}{\frac{s_{d}}{\sqrt{n}}} $$

其中 $ s_d $ 是 sample standard deviation of differences。

alt text

Test of variances

对于单个variance的测试，使用的是卡方分布：前提：population是正态分布。需要注意卡方分布没有t分布那么宽容，不能“近似正态”，必须是正态。 $\chi^2=\frac{(n-1)s^2}{\sigma_0^2}$ 对于两个variance之间的测试，使用的是F分布。例子包括对比不同时期的variance，或者对比baskets of securities和indexes。前提也是两个population都是正态分布，也是严格要求正态；两个sample要independent。 $F=\frac{s_1^2}{s_2^2}$ 如果要靠表格来知道critical values，通常会将两个variance中的较大者用来做分子（以减少表格数）。结合图来确定符号和critical value的关系：

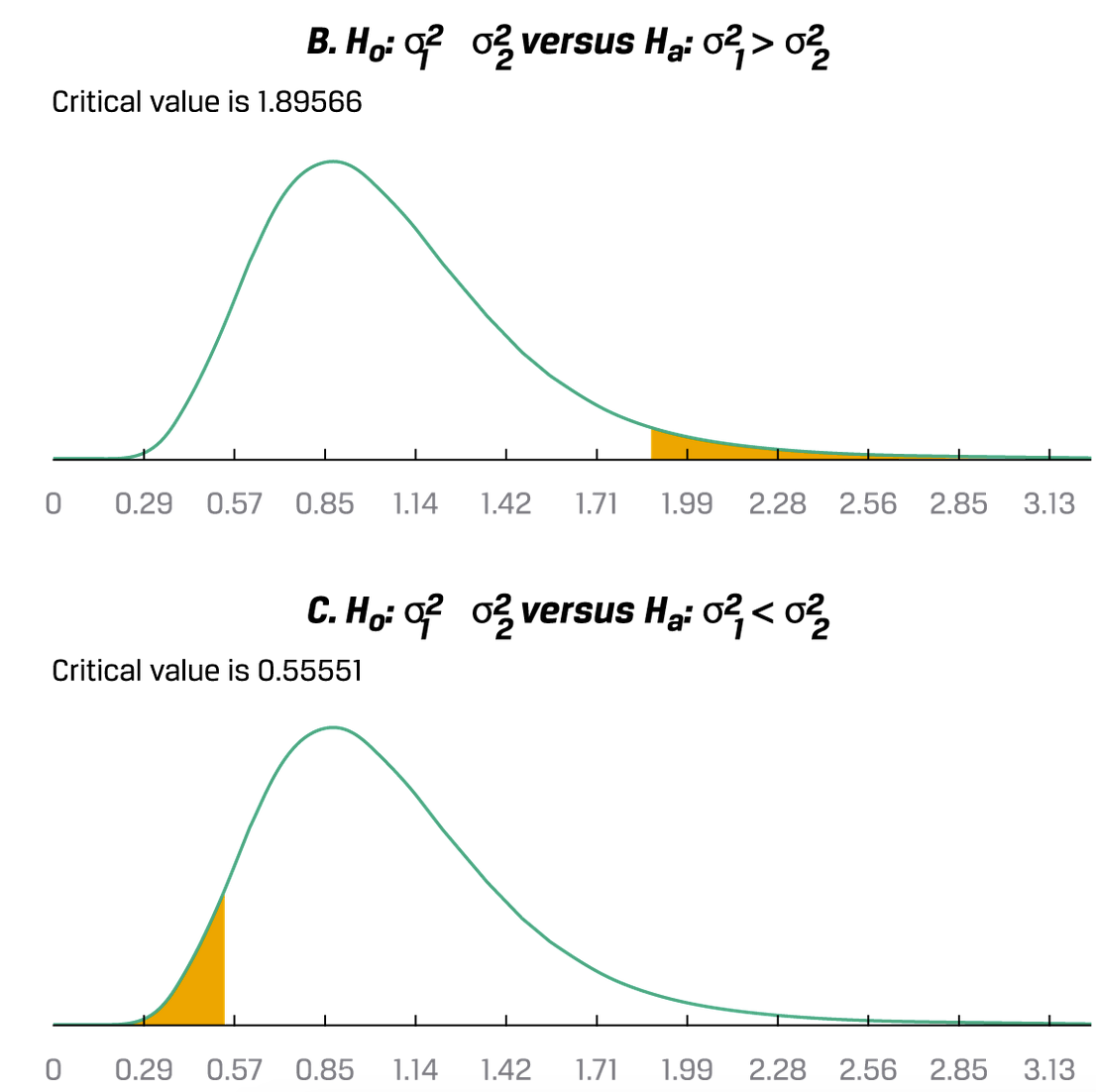
Alt text

Level of Significance

Type I error: false reject（reject 了 true 的 null）

Type II error： fail to reject（没有reject false的null）

Level of significance是对于发生Type I error的风险容忍度，用 $ \alpha $ 来表示；而 $ 1-\alpha $ 就是 confidence level。

降低 $ \alpha $ 就会导致更容易发生Type II error。只有提高样本容量才能同时降低两种error。

Power of a test是正确地reject了false null的probability，用 $ 1 - \beta $来表示。

State the Decision Rule

确定critical values，对比计算出来的statistic来决定是不是reject the null，所谓的statistically significant。

以z-score为例，双侧的时候是 $ ± z_{\alpha /2} $ ，单侧则是 $ z_{\alpha} $ 。对于判断是否reject，既可以对比计算出来的z值和critical value的值（$ z = \frac{\bar X - \mu_0}{\frac{\sigma}{\sqrt{n}}} $ 与 $ ± z_{\alpha /2} $ 对比），也可以对比hypothesized parameter是否落在confidence interval之外（$ \bar X ± z_{\alpha /2}\frac{\sigma}{\sqrt{n}} $ 和 $\mu_0$）。

Collect Data and Calculate

  1. 需要确定sample过程没有bias，比如sample selection或time-period bias
  2. 需要对数据进行清理，检查不准确的、测量错误。

Make Decisions

Decision分两部分，一个是统计上是否reject，另一个则是基于统计的decision所做的economic decision。

例如在样本非常大的时候，可能 $ \mu_0 = 0 $ 很容易就reject了，但是这种规模的投资组合是无法实现的。

P值

P值的定义：落在 计算出来的z值（或其他统计量）之外的区域的面积占比。

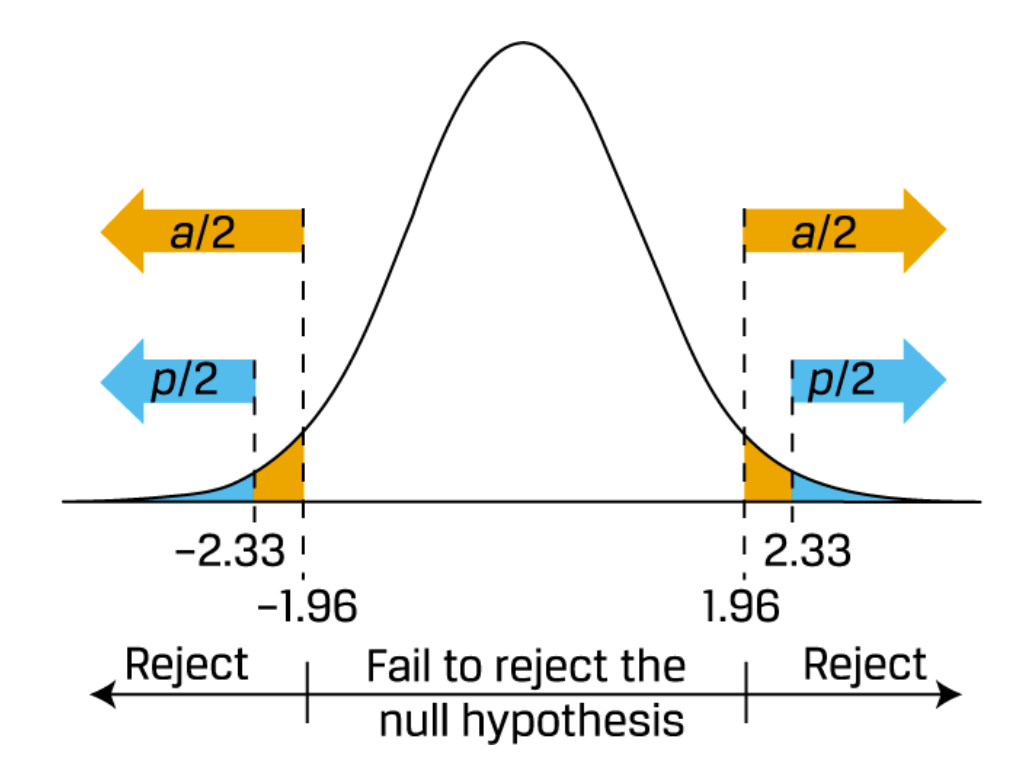
Alt text

计算：相当于要算CDF。例如，对于z-dist来说，如果z值是2.33，那么用excel算就是：(1-NORM.S.DIST(2.33,TRUE))*2

p值越小，就越可能是reject null。通常跟 $ \alpha $ 比较，如果p值小于$\alpha$就可以reject。

BH False Discovery Approach

重复抽样可能会导致增加Type I error，对于p值可以使用BH来adjust，流程是：

  1. 按p值由低到高排列
  2. 按顺序计算 $ \alpha \frac{第i个}{进行的test总数} $ 并跟对应的p值比较，其中：
    1. $ \alpha $是显著性水平
    2. 第i个是指从低到高排列中的第几个
    3. 进行的test总数是test不是sample size
    4. 终止条件是$ p_{i} \ge \alpha $
  3. significant的是这些之中 $ p_{i} \le \alpha \frac{第i个}{进行的test总数} $的

比如：

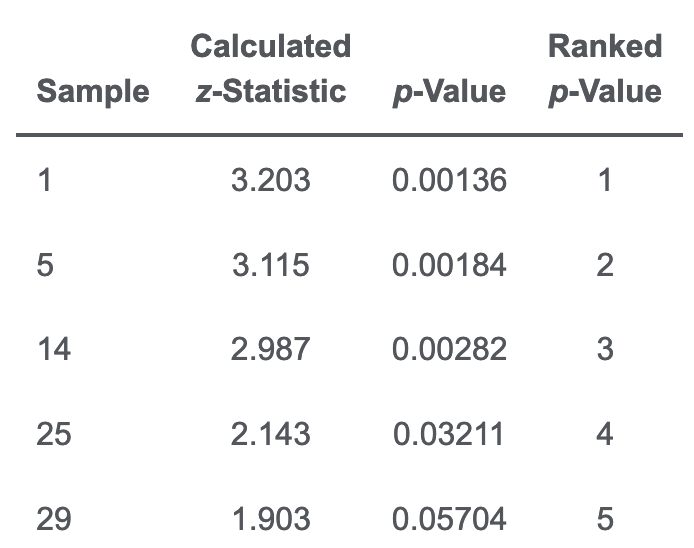
Alt text

该例$ \alpha = 5\%$，所以到第5个的时候p已经大于5%了，就停止了。

在做hypothesis test和确定critical values的时候，默认前提是test只在这些data上run了一次；对相同data多次test会导致data snooping。

目录