CFA-08 衍生品

于 2024-05-02 发布

基础概念

  1. 衍生品中的底层资产叫underlying。
    1. Market participants use derivative agreements to exchange cash flows in the future based on an underlying value.
    2. 衍生品transform底层资产的performance，而不是pass through
  2. 衍生品交易通常会涉及至少一个金融中介作为counterparty
    1. counterparty 信用风险：交易对手无法履行合同项下财务义务的可能性。
  3. settlement：the closing of the transaction，指交易关闭
  4. maturity：到settlement的时间长度
    1. 每个合约都有一个期限
  5. buyer指与持有底层资产的损益同向的那个；seller则是与底层资产反向的那个
  6. contract size 可以constant也可以变化
  7. stand-alone derivative和embedded
    1. 嵌在underlying里面的是embedded，比如callable bond中的那个就是
  • firm commitment：一个预先确定的金额会在settlement的时候交换
    • 比如远期合约、期货合约等
  • contingent claim：其中一个counterparty决定是否以及何时settle
    • 比如期权

使用衍生品，可以：

  1. 做空
  2. 组合多元化
  3. 调整（offset）来自某个交易中包含的敞口
  4. 用较少的钱（relatively small cash outlay）创造更大的敞口
  5. 衍生品通常比基础现货市场交易的交易成本低、更具流动性

分类

根据底层资产的类型：

  • 股票（equity）
    • 个股的衍生品通常是期权
    • 指数衍生品则有：期权、远期、期货和掉期；期权、期货和掉期是基于realized volatility的
  • 固定收益（fixed income）
  • 利率（interest rates）
    • 利率掉期，通常用作把fixed变成floating
    • 各种MRR常用作underlying
  • 货币（currencies）：用来控制汇率风险
  • 商品（commodities）：既可以是用来控制价格风险，也有可能是避免物理交割地炒
  • 信用（credit）

市场

OTC市场的特点是dealer做market maker；合约可以自定义，满足特定的需要。

ETD（Exchange-Traded Derivative）交易所：

  1. 都是标准化合约，合约内容由交易所确定（交易成本更低）
    1. 由于是标准化合约，Dealer通常能同时买卖赚差价
  2. 需要存入抵押品，交易所提供针对交易对手违约的保证
  3. 透明度：交易需要向交易所和国家监管机构公开

金融危机之后，对于OTC市场很多监管机构要求设置central clearing。CCP（central counterparty）为大多数衍生品合约提供清算和结算。investor和issuer仍然受益于OTC市场的灵活性；而他们的counterparty（金融中介）之间的清算结算则更类似ETD市场。但是系统性风险（systematic risk）也从金融中介转移到了CCP上。

以利率互换为例：

  1. 衍生品交易在 swap execution facility (SEF) 上执行
  2. 原始交易信息提交给 CCP
  3. CCP用identical trades替换原始的SEF交易（ novation process ）

如果对手方是CCP，那么需要担心的不是CCP违约： alt text

远期、期货、互换

这一类都是firm commitment，特点是：

  1. 确定的规模
  2. 确定的底层资产
  3. 在特定的未来日期或多个日期进行现金流量或标的物的一次或多次交换
  4. 交换基于提前商定的价格（pre-agreed price）

由于这类衍生品的收益是线性的，所以也叫 linear derivatives 。

期货

期货的特点是 mark to market（MTM），也就是daily settlement，每天结算gain or loss（从保证金账户里面扣或加）。交易者需要存inital margin并且保持maintenance margin。投资者必须跟金融中介交易，金融中介再跟clearinghouse交易：

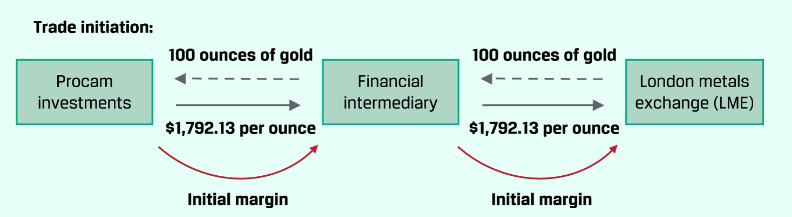
alt text

回忆margin call的公式：

$$ 触发价格=\frac{杠杆提供的资金占的初始价格}{1-\text{maintenance margin}} $$

交易所控制信用风险的手段：

  1. 保证金（除了通用的保证金比例之外，交易所对于某些交易可以要求更高的比例）
  2. price limit，限制价格区间
  3. circuit breaker，熔断

到期的时候还outstanding的合约的数量，叫做open interest。

互换

Swap。通常是两方，一个给fixed-rate的，另一个给浮动的。floating-rate payer、fixed-rate payer。

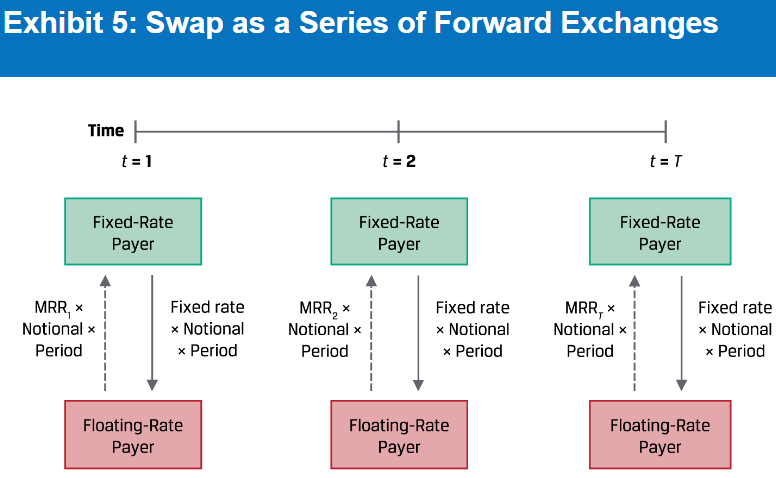
alt text

通常不会像图中这样全额互换，而是只换差价。

互换开始时是不交换现金的，所以开始时的价值是0；随着时间，MTM之后就会出现一正一负。如果涉及CCP，那么也会有类似期货的保证金制度。

期权

期权也是：指定标的物、指定规模、预先商定的执行价格、确定的到期日。期权买家是有权利但不是义务行权，所以payoff是0或正数（注意不是profit）。

在计算收益时，gain是市价-行权价；net是gain-premium。以call option为例，行权价40，市价45，期权费6，那么买家是net loss=5-6=-1，卖家是net gain=-5+6=1。注意卖家甚至是正的。

期权合约的元素可以是OTC上各方商定的（自定义）；也可以是交易所的标准化的。

在到期之前，（call）期权的价值：

  1. 如果市价大于行权价，那么内在价值是 市价-行权价，期权叫做in-the-money
  2. 市价等于甚至小于行权价，那么内在价值都是0，小于叫做out-of-the-money，等于叫做at-the-money

买家： alt text

收益图显然跟firm commitment的不同，所以这类contingent claims也叫做non-linear derivatives。

期权的time value始终是正的，在到期的时候降到0.

（信用风险）在买家支付了期权费之后，卖家就不再有来自买家的风险exposure；但是买家始终有来自卖家的exposure，等于到期时的payoff。（卖家可能跑路，所以只有short的可以default）

信用衍生品

credit derivative。经典的CDS，按照CDS credit spread来交易，这个又根据POD和LGD来确定。

但是CDS虽然叫swap，实际上是contingent的。和利率互换一样，本金是不交换的，只是作为计算基础。

alt text

除了买CDS当做买保险来控制风险敞口之外，也有投资者是为了gain from higher credit spreads买的，这些人相当于对信用风险持有short。无论什么情况，seller都是对信用风险持有long的。

买方是定期向卖方支付这个fixed spread payment的。

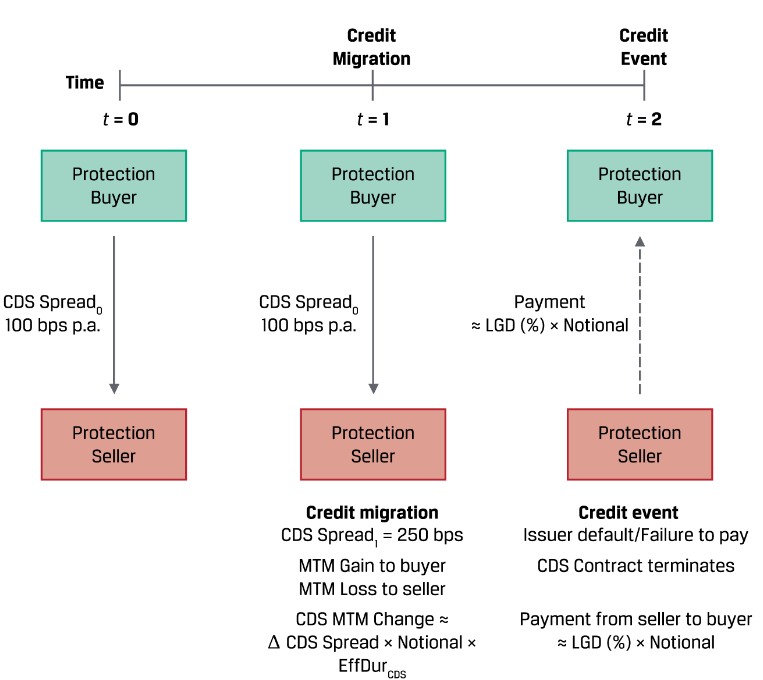
alt text

衍生品的好坏

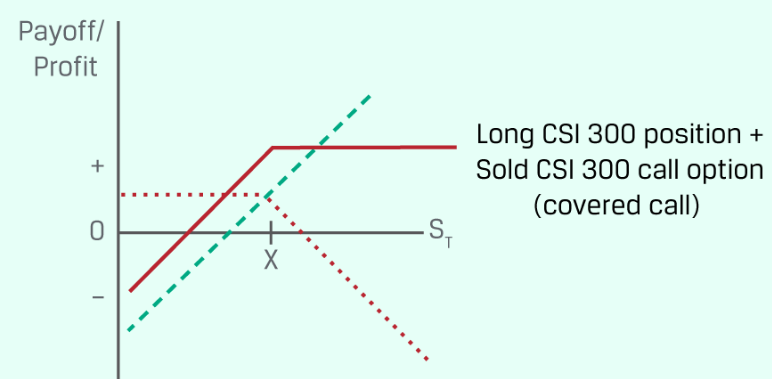
covered call：long底层资产，同时sell 一个call option；收益图： alt text

  • 控制、转移风险
  • 信息发现
    • 衍生品价格可以作为底层资产价格变动方向的一个参考（价格发现）
    • 期权价格包含了底层资产的隐含波动率（implied volatility）
  • operational advantages
    • 交易成本低：物流仓储保险
    • 流动性更高
    • 立刻需要支付的（upfront）现金要求低（比起买卖底层资产来说）
    • 可以卖空
  • 提高市场效率

坏处：

  • 更高的杠杆
  • 复杂度提高，导致参与者不能完全了解风险
  • basis risk：衍生品的预期价值（expected value）与标的资产的预期价值出乎意料地不同
  • 流动性风险：比如MTM不够钱补仓（cash flow timing）
  • MTM带来的更频繁的风险敞口监控和管理（信用风险）
  • 系统性风险

用途

发行人

会计规则：

  1. 要on balance sheet，使用fair market value
  2. 在income statement上，要根据MTM通过earning报告，除非是embedded的
  3. 如果是符合hedge会计准则的，可以用来offset，来降低波动性
    1. Cash Flow hedge：吸收浮动利率资产或负债的可变现金流（比如利率互换、外汇远期）
    2. fair value hedge：如果一个衍生品是用来offset一个资产或负债的fair value波动的（比如利率互换、商品（库存）远期）
    3. net investment hedges：offsetting the foreign exchange risk of the equity of a foreign operation（货币互换、货币远期）

衍生品的MTM损益保存在OCI下的一个权益账户里，在底层资产交易确认的时候释放。

由于使用目的，所以多数需要用OTC柜台来自定义合约。

投资者

  • 复制cash market策略
  • 对冲（hedge）基金价值（fund’s value） 以应对底层资产的不利变动
  • 改变或添加风险敞口（exposures）

更多是在ETD市场交易。

定价

套利

有两种思路:

  1. 两种相同现金流的资产在相同时间的价格必须相等（law of one price）
    1. 比如两个zero-coupon，t=1的时候都是100；那么t=0的时候如果价格不等，就可以套利
  2. 确定的未来价格的资产在t=0的时候必须以discount rate = risk-free rate的现值进行交易
    1. 对于多数投资者，discount rate应该是repo rate

复制定价

replication：long实物头寸+short远期 的现金流跟 以risk-free借入购买实物头寸需要的现金并购买实物头寸 的现金流是一致的。

risk-free rate就是机会成本。

如果有持有成本（cost of carry）。如果在机会成本之外，持有实物头寸还产生了其他持有成本，远期价格就应该更高以补偿持有者；相应的，如果持有产生了收益，远期价格就应该更低。根据连续复利还是离散有两条公式，进行相应的调整：

$$ F_0(T)=[S_0-PV_0(I)+PV_0(C)](1+r)^T\\ F_0(T)=S_0e^{(r-i+c)T} $$

连续复利的式子里，持有收益（income）和成本（cost）都是以rate的形式。

外汇

外汇远期，比如 long USD/EUR 的意思是到期卖出美元、买入欧元。在复制定价的时候，本币和外币有不同的risk-free rate。注意，算外汇定价的时候需要用连续复利。直接记公式：

$$ F_{0,f/d}=S_{0,f/d}e^{(r_f-r_d)T} $$

alt text

如果 $ r_f - r_d < 0 $ ，那么外币就称为trade at premium。

alt text

注意，Foreign Currency Forward和FX forward不是一个东西。比如 $ r_f < r_d $ ：

  1. 那么显然 $ F_0 < S_0 $ 的，但是这说的是FX forward，所以FX forward是discount
  2. 而外币趋向贬值，所以对于Foreign Currency Forward是 $ F_0 > S_0 $ ，是premium

A fixed-coupon bond priced at par whose coupon is above the risk-free rate，$ F_0(T) < S_0 $

convenience yield

持有physical商品比持有衍生品得到的非现金收益。如果远期价格明显低于无套利价格（Spot价格），就可能是convenience yield。

中间的日期的定价

期货

一个通用记忆是：seller是以 $ F_0(T) $ （或其现值）卖出，以 $ S_t $ 购入的，所以收益是F-S；buyer是反过来，S-F。收益分析做好对应就行。

起始日的定价是：

$$ F_0(T)=S_0(1+r)^T\\ S_0=F_0(T)(1+r)^{-T} $$

对于中间的日期的定价，则是 $ F_0(T) $ 在那一天的现值与那一天的现价的差别，以long的角度看：

$$ V_t(T)=S_t-F_0(T)(1+r)^{-(T-t)}\text{，其中t < T} $$

$ V_t(T) $ 大于0，long的gain、short的loss。

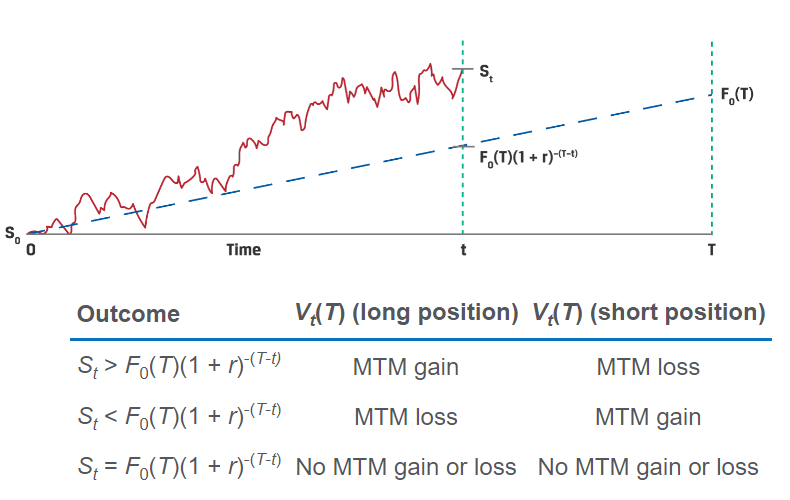
alt text

如果再把持有收益和成本加上：

$$ V_t(T)=(S_t-PV_t(I)+PV_t(C))-F_0(T)(1+r)^{-(T-t)}\text{，其中t < T} $$

注意，这种题不需要考虑第一次已经付的利息，只需要考虑t=4的时候，下一次付息（这里是t=6会付一次）的现值： alt text

外汇

$$ V_t(T)=S_{t,f/d}-F_{0,f/d}(T)e^{-(r_f-r_d)(T-t)} $$

利差扩大会导致外币在远期的角度上贬值、本币在远期的角度上升值。

这条公式是对于未来买入d卖出f的角度的。

alt text

  1. 首先不通过计算判断是gain还是loss：新的S↘，那么对应的F↘；我是持有ZAR的，站在t=T的时间点，同样的ZAR按市场价能够换到更多的EUR；但是远期合约锁死了，我要以更高/不利的汇率换成EUR；所以我是loss
  2. 计算：loss的金额是16.909-16.5

存在期限结构的定价

利率、信用利差、外汇等都有期限结构。

第一步是将coupon转换成zero-coupon。比如：

期限 coupon PV
1 1.5% 99.125
2 2.5% 98.275
3 3.25% 98.000

算出对应期限的zero-coupon的流程：

$$ 99.125=\frac{101.5}{(1+z_1)^1}\\ 98.275=\frac{2.5}{(1+z_1)^1}+\frac{102.5}{(1+z_2)^2}\\ 98=\frac{3.25}{(1+z_1)^1}+\frac{3.25}{(1+z_2)^2}+\frac{103.25}{(1+z_3)^2} $$

依次算出 $ z_1、z_2、z_3 $ 。这个过程也叫bootstrapping。每个z都对应一个discount factor：

$$ DF_i=\frac{1}{(1+z_i)^i} $$

discount factor：The present value of a currency unit on a future date

本质上这里也在重复之前的IFR（隐含远期收益率）；使用0y1y, 1y1y, 2y1y等算未来的收益率。

但是如果是月收益率，比如给出3个月和6个月的，需要算3m3m，就要先做转换，把periodicity同步。比如3个月1.25%，6个月1.75%：

  1. 6个月的periodicity是2，3个月的是4，所以先把6个月的转换成periodicity是4的： $ (1+APR_4/4)^4=(1+1.75\%/2)^2 $，得到1.74619%
  2. $ (1+1.25\%/4)^1\times(1+IFR_{3m,3m}/4)^1=(1+1.74619\%/4)^2 $
    1. 特别注意这里的IFR是除以了4的，不然半天算不对

alt text

FRA

Forward Rate Agreements，OTC衍生品：

  1. 假设本金在未来某个时间开始（A）到某个时间结束（B）存定期存款；
  2. t=0时，根据 $ MRR_{0,A} $ 和 $ MRR_{0,B} $ 计算出 $ IFR_{A,B-A} $ ，这就是buyer（fixed-rate player）用的利率
  3. 当时间走到t=A时，确定此时的 $ B-A $ 长度的MRR， $ MRR_{B-A} $，这就是seller（floating-rate player）用的利率
  4. 用 $ (MRR_{B-A}-IFR_{A,B-A})\times 本金 \times 期间 $ 计算出对于buyer而言的、t=B的净支付额
  5. 把对于buyer而言的、t=B的净支付额以 $ MRR_{B-A} $ 折现成t=A时的PV，进行settle

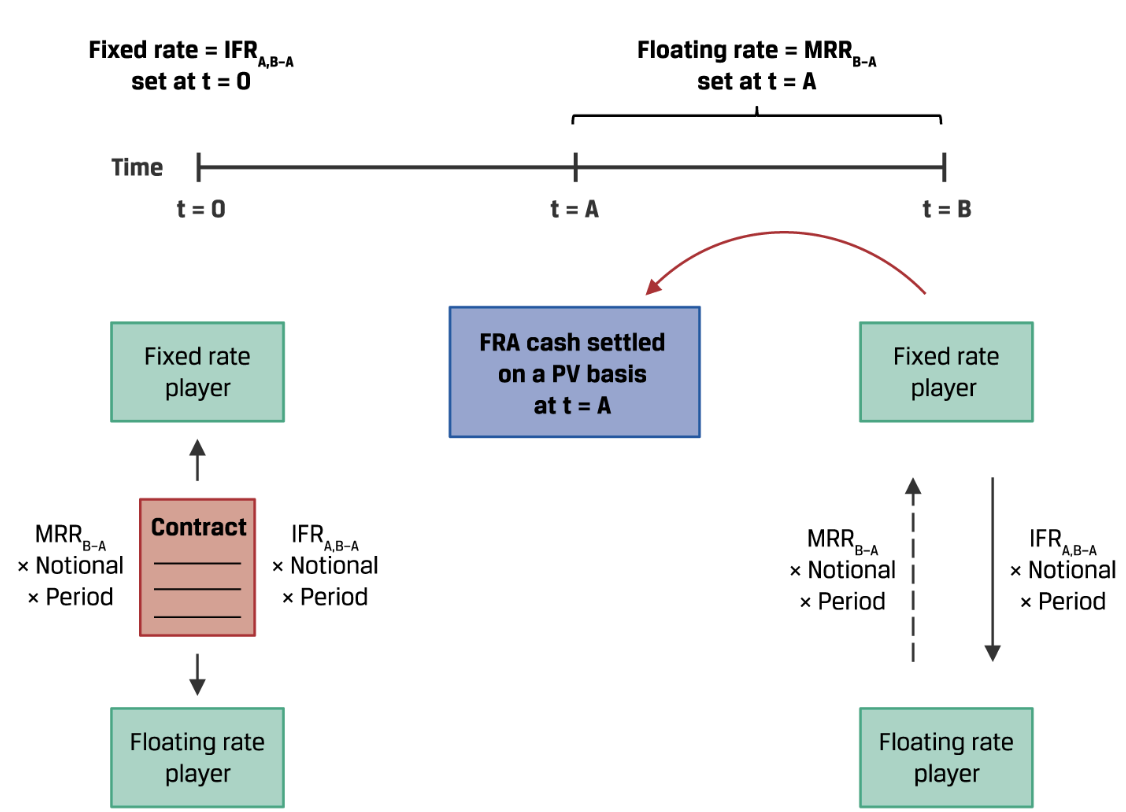
alt text

所以FRA是在目标期间开始时settle的，不是在结束时。例子：

alt text alt text

注意这里用的是MRR直接除以4，不是四分之一次方。

FRA基本上都是由金融中介用的，用来管理它们资产负债表上的利率敏感资产和负债。而利率掉期才是投资者和发行人常用的利率风险管理工具。

注意说法，“on a one-month AUD MRR in three months’ time”是3,1不是1,3。

期货合约定价

远期每天都把contract value重置为0，每天都有一个contract MTM，但是只有到期那天的MTM是真的settle的（所以每天的realized MTM都是0）。

期货则不一样，开始时就要initial margin；中间还要maintenance margin。contract value是会变的，每天都有realized MTM，而contract MTM重置为0。

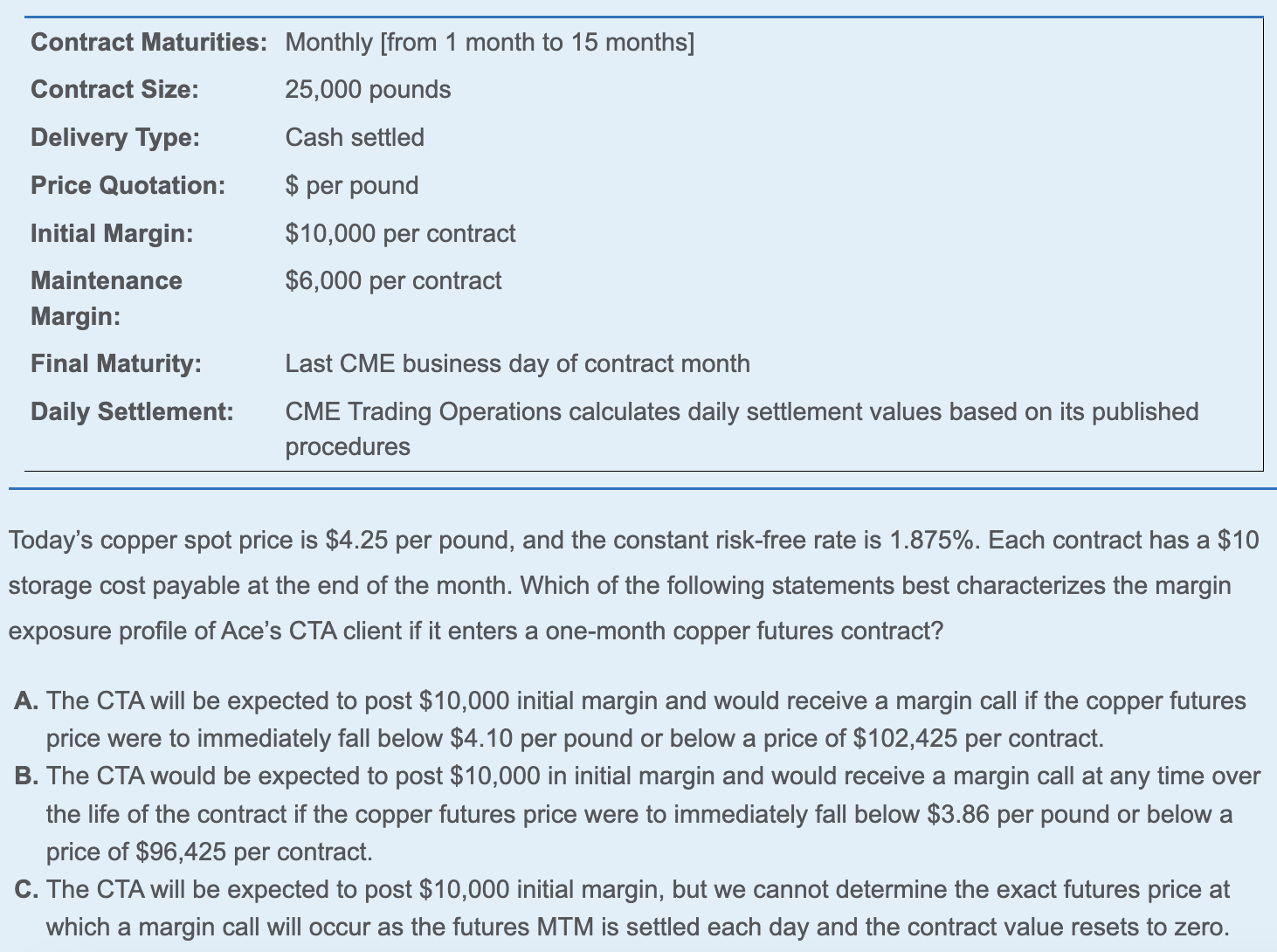
持有成本对于计算的影响： alt text

initial和maintenance之间差了4000，所以只要每磅价格下跌 $ 4000/25000 = 0.16 $ 就会触发margin call。

接下来计算 $ f_0(T) $ 以便得到call price：

$$ f_0(T)=[S_0+PV_0(C)]\times (1+r)^T\\ PV_0(C)=10\times(1+1.875\%)^{-\frac{1}{12}}=9.98\\ f_0(T)=(4.25\times 25000+9.98)\times (1+1.875\%)^{\frac{1}{12}}=106425\text{ per contract}\\ \text{call price}=(106425-4000)/25000=4.10 $$

利率期货是以价格进行交易的（不是以利率）：

$$ f_{A,B-A}=100-(100\times MRR_{A,B-A}) $$

也就产生了futures contract basis point value (BPV)：

$$ BPV=名义本金\times 0.01\% \times 期间 $$

同样也是在t=A的时候settle。比如： alt text

但是跟FRA不同的是：

  1. long 期货合约：MRR下跌，price上升，gain
  2. short 期货合约：MRR上升，price下跌，gain
  3. FRA的settlement需要折现，而期货不需要（直接用BPV乘以点数）

FRA的fixed-rate payer等同于short期货合约。

如果1）利率不变，或者2）期货价格跟利率变化是uncorrelated，那么期货和远期的价格是相同的；否则：

  1. 如果期货价格跟利率positive相关，那么期货价格>远期，因为期货每天settle导致收益可以以更高利率再投资
  2. negative，就小于

大多数期货合约的期限较短，并且大多数市场参与者能够在这些期限内以接近无风险的利率借入资金，通常会导致期货和远期价格之间几乎没有区别。除非convexity bias；期货的变化是线性的，而FRA的不是。

alt text

CCP

CCP的存在对于OTC市场的远期合约也引入了类似的保证金机制。但是远期依然是远期，MTM在到期日才会realized，所以以下AB都是错的：

alt text

互换

FRA在period开始时settle，而利率互换在period结束时settle。FRA在不同期限有不同的IFR（固定利率），但是利率互换用相同的IFR计算所有现金流。

利率互换的IFR用的是par rate计算，就是算PMT的那个，但是有所不同：

$$ \Sigma \frac{IFR_{i}}{(1+z_i)^i}=\Sigma \frac{rate}{(1+z_i)^i} $$

比如一个3期swap，已知 $ IFR_{0,1}、IFR_{1,1}、IFR_{2,1} $ 和对应的zero-coupon的z，就可以得到互换的rate：

alt text

作为收MRR付IFR的那个，支付的金额计算依然是：

$$ \text{net payment}=(MRR-IFR)\times本金\times期限 $$

两者都有对称的payoff特征，都是以差额settle，都有counterparty 信用风险。

alt text

Gain和loss就是看浮动利率payment的现值和固定利率payment现值之间的比较。

alt text

在第一次settlement之前，是没有足够信息确认谁gain谁loss的；swap在整个生命周期内总体而言是 $ PV(floating)=PV(fixed) $ 的，所以如果第一次settlement的时候（其他因素不变），一个要给钱出去，那么它的未来现金流就需要更高来补偿这次settle的是负数，所以是MTM gain。

floating-rate payer就跟long 固定利率债券一样，所以投资组合经理如果做floating-rate payer就是在延长久期。

期权

期权的价值由 行权价、标的物价格、时间价值 组成。

在可以行权但是还没有到maturity的时候（t < T），则是对比现价 $ S_t $ 和 行权价的现值：

$$ X(1+r)^{-(T-t)} $$

对于看涨期权，期权价值（exercise value）就是 $ Max(0,S_t-X(1+r)^{-(T-t)}) $ 。

moneyness

就是之前提到的 in-the-money、at-the-money和out-of-the-money。moneyness通常用来对比同一个标的资产的不同期权。

deep-in-the-money指非常有可能行权的期权状态，期权的价格几乎跟标的资产1:1变动；而deep-out-of-the-money指非常不可能行权，价格就没有那么敏感。

时间价值

虽然欧式期权只有到期才能行权，但是之前对于到期前的价值讨论也是有用的，因为可以在到期前卖掉或买一个，交易价格（ $ p_t 或 c_t $ 来标记）反映了未来的expected payoff。

  1. 相同的volatility，更长的时间代表更大的价格散布可能，所以increase价值
  2. 相同的时间，更大的volatility，increase价值

time value始终是正的，在到期时降到0，叫做time value decay。对于购入的期权，decay是成本；对于卖出的期权，decay是收益。

alt text

上下限

对于看涨期权，期权价格的下限是exercise value，上限是标的资产现价：

$$ Max(0,S_t-X(1+r)^{-(T-t)})< c_t \leq S_t $$

看跌期权：

$$ Max(0,X(1+r)^{-(T-t)}-S_t)< p_t \leq X $$

把 $ p_t和c_t $ 看成期权费，移到一边就更好理解了：

  1. 看涨期权，只有资产现价大于行权价的PV且cover了期权费，买家才会净赚，才会买；如果期权费太贵，那还不如直接买标的资产
  2. 看跌期权，只有资产现价低于行权价的PV且cover了期权费，买家才会净赚，才会买

复制定价

replicate。

对于看涨期权：

  1. 开始时相当于以无风险利率借入一个金额、以 $ S_0 $ 购买底层资产
  2. 到期的时候
    1. 如果结果是行权，就是以 $ S_T $ 卖掉资产、还行权价 X 那么多的钱
    2. 否则不需要settle

但是因为资产的价格是不确定的，所以不是借 $ X(1+r)^{-T} $ 那么多，而只是借a proportion of，proportion基于到期时的行权可能性（likelihood）。

所以与firm commitment不同，期权的复制交易需要根据行权可能性不停调整（adjust）。

对于看跌期权：

  1. 开始时相当于以 $ S_0 $ 卖出资产，把proceed以无风险利率借出
  2. 到期时
    1. 如果结果是行权，就是用出借资金的收益以 $ S_T $ 购买资产
    2. 否则不需要settle

影响价格的因素

  1. 底层资产价格
  2. 行权价
  3. 期限
    1. 对于看涨期权，时间越长value越高
    2. 对于看跌期权，需要注意有的情况下因为payoff是等于卖掉资产实现 $ X- S_T $ 的，所以时间越长反而有可能降低PV
  4. 无风险利率
    1. 由于exercise value是行权价的现值跟资产现价的对比，所以如果exercise value大于0的话，利率越高，PV越小；看涨期权价值变大，看跌期权价值变小
    2. 对时间价值没有直接影响
  5. 底层资产价格的波动性
    1. 波动性越大，time value越大；否则越小
    2. 时间价值增加，就会推高期权价
  6. 直接持有资产的收益和成本
    1. 把call option的buyer视为不持有资产的，所以income降低value、cost增加value；put就反过来

Put-call parity

fiduciary call：t=0时以 $ c_0 $ 购买一个call option，同时投资 $ X(1+r)^{-T} $ 购买一个risk-free bond。

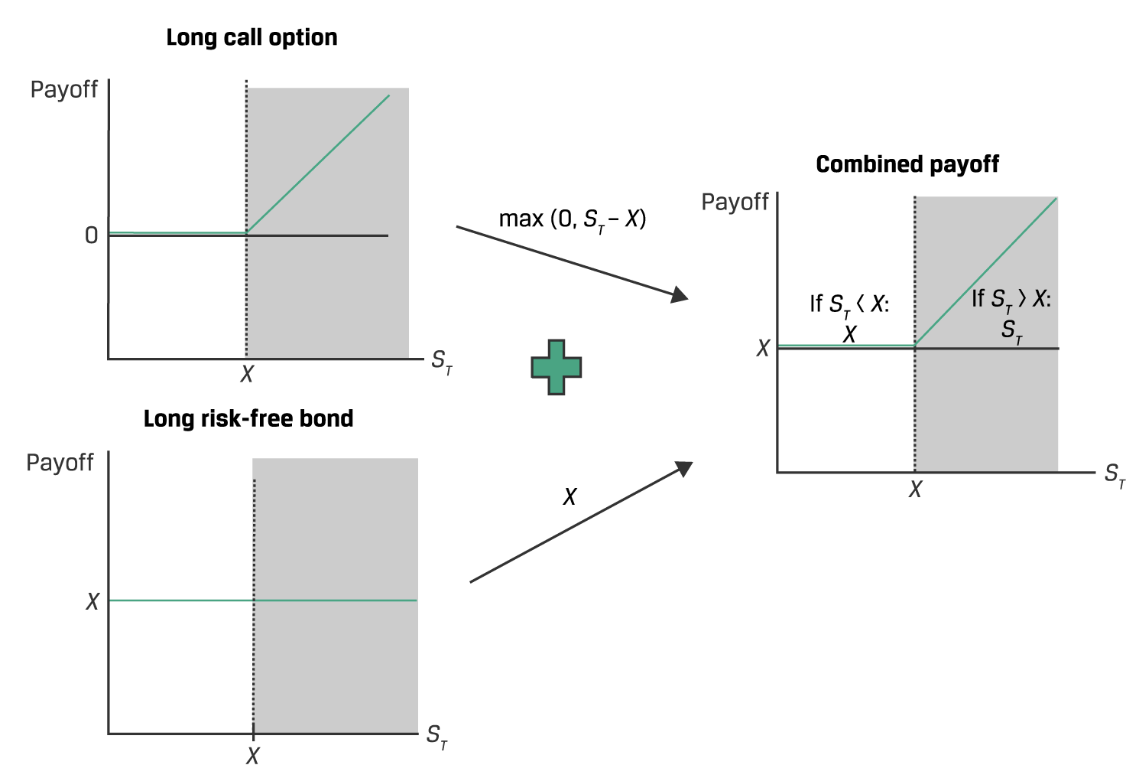
alt text

protective put：t=0时以 $ S_0 $ 购买底层资产，同时以 $ p_0 $ 购买一个put option。

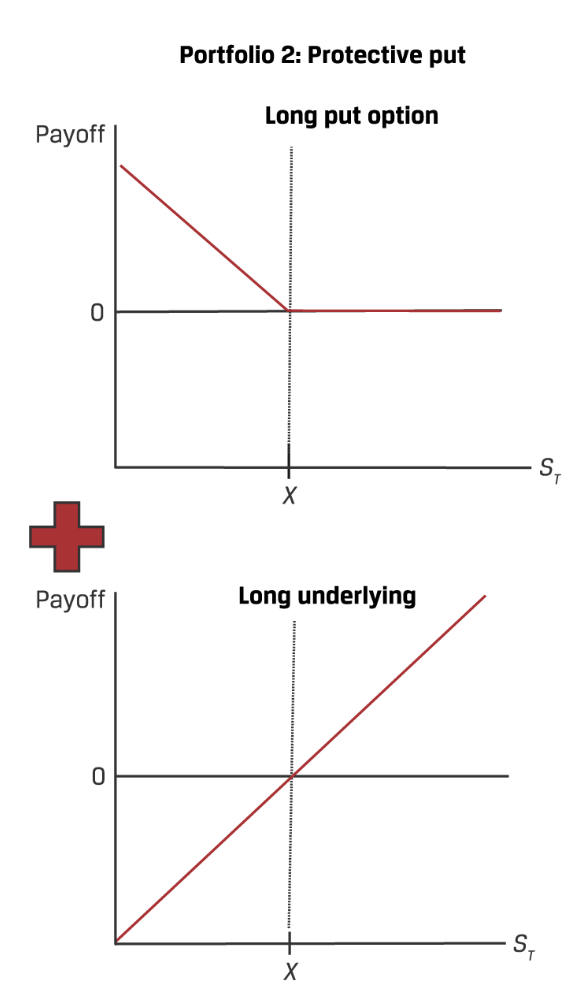
alt text

parity：

$$ S_0+p_0=c_0+X(1+r)^{-T} $$

把一边留得只剩一个元素，另一边的每一项的符号就代表long还是short，同时也代表着如何复制那一个元素的payoff情况。比如

$$ S_0=c_0+X(1+r)^{-T}-p_0 $$

就代表着底层资产的收益情况可以用long call option、long risk-free bond、short put option来复制。

covered call strategy：long底层资产+卖出call option。

虽然我很不认同，这里明明写的是expire而不是mature，但是意思就是到期时in-the-money，所以显然是B： alt text

put-call forward parity

将 $ S_0 $ 换成远期合约的 $ F_0(T)(1+r)^{-T} $ ：

$$ F_0(T)(1+r)^{-T}+p_0=c_0+X(1+r)^{-T} $$

意思是在t=0的时候，买入一个远期合约+一个面值是远期价格 $ F_0(T) $ 的无风险bond。

左边叫做synthetic protective put，因为用远期+bond的组合合成了一个底层资产。如果T时底层资产是增加了的，那么：

alt text

$$ p_0-c_0=[X-F_0(T)](1+r)^{-T} $$

long put + short call = long 无风险bond + short 远期

对于公司而言

  1. 股东可以视为：long公司这个资产（ $ S_0 $ ），而且purchased了一个行权价是Debt、标的是公司价值的看跌期权 （ $ p_0 $ ）
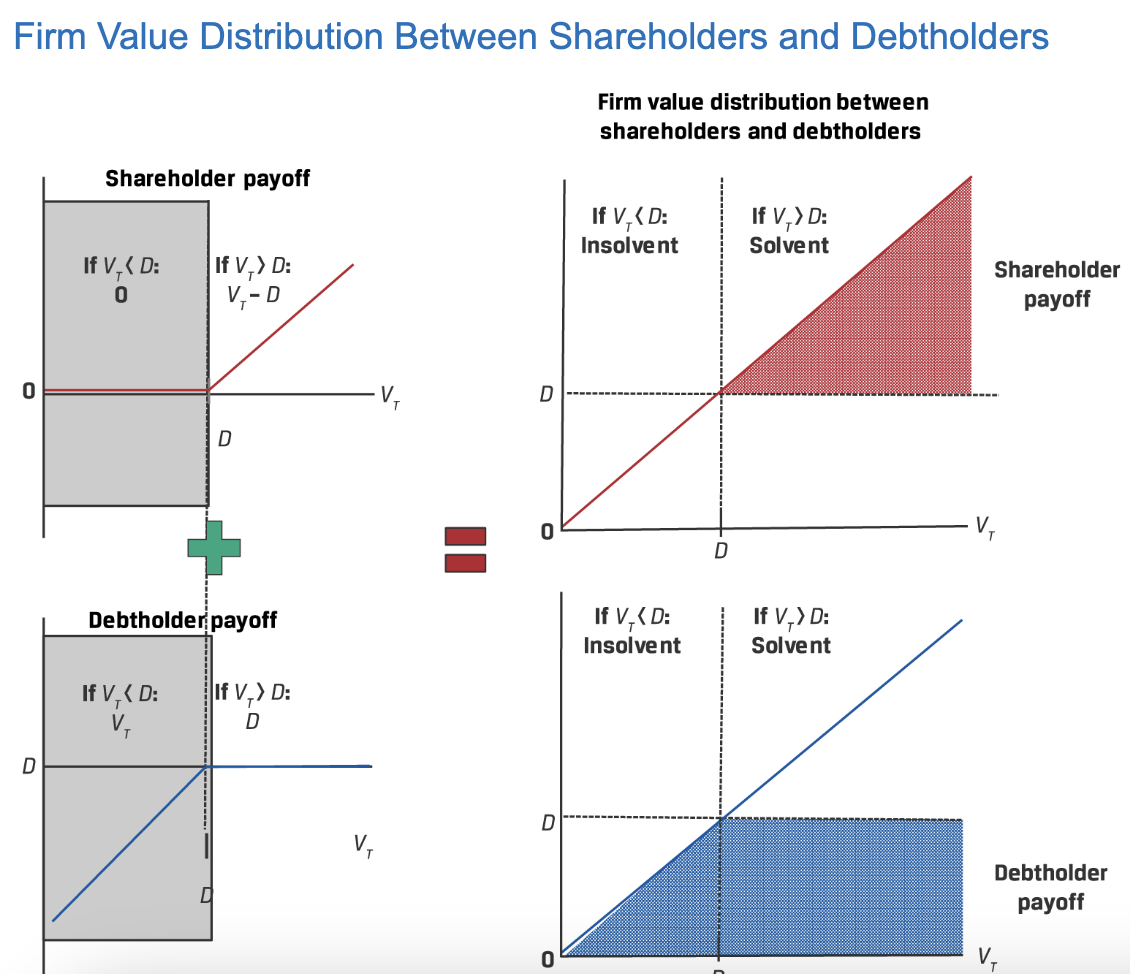
  2. 债权人可以视为：long一个无风险bond，而且sold了一个行权价是Debt、标的是公司价值的看跌期权 alt text

$ p_0 $ 可以视为债权人因为公司可能存在资不抵债的场景所以要求股东提前支付的期权费。

公司leverage提高可以看做看跌期权价值增加，股东收益、债权人受损。

二元定价

binomial valuation。

假设现在的价格是 $ S_0 $ ，未来要么上升 $ S_1^u $ 要么下降 $ S_1^d $ 。上升下降的概率q是不需要知道的，只需要确定 $ S_1^u 和 S_1^d $ ，也就是 spread，或者叫volatility。

另外需要假设行权价X满足：$ S_1^d < X < S_1^u $

t=0 t=1,up t=1,down
$ S_0 $ $ S_1^u $ $ S_1^d $
$ c_0 $ $ c_1^u $ $ c_1^d $
  $ R_1^u $ $ R_1^d $

上升下降对应的收益R：

$$ R^u=S_1^u/S_0\\ R^d=S_1^d/S_0 $$

对应的期权价值 c：

$$ c_1^u=Max(0,S_1^u-X)\\ c_1^d=Max(0,S_1^d-X)\\ $$

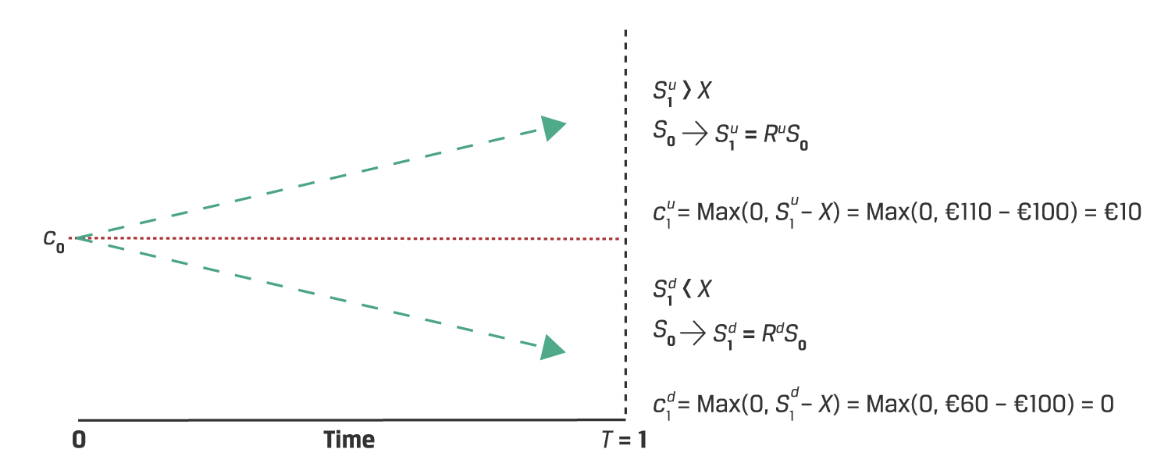
alt text

接下来就是计算一个h（指t=0时购买的底层资产数量），使得无论t=1时价格是上升还是下降，组合的价值都不变：

$$ V_0=h\times S_0 - c_0\\ V_1^u=h\times S_1^u - c_1^u\\ V_1^d=h\times S_1^d - c_1^d\\ V_1^u=V_1^d\\ h=\frac{c_1^u-c_1^d}{S_1^u-S_1^d} $$

h也叫hedge ratio，代表每卖出一个call option需要购买的底层资产的单位量。

另外，由于无论价格上升还是下降，t=1时价值都是 $ V_1 $，那么 $ V_1 $ 和 $ V_0 $ 之间还存在这样的关系：

$$ V_0(1+r)=V_1 $$

也就可以求出c0了。

所以：

  1. 底层资产的上升或下降的actual probability是无关的

如果h是正的，那么代表着一买一卖；如果是负的，就是同时买或者卖。如果期权现价跟无套利定价不一样，可以这样算应该怎么操作：

alt text

  1. 用 $ h=\frac{p_1^u-p_1^d}{S_1^u-S_1^d} $ 算出h
  2. 根据h的符号确定是一买一卖还是同时买，然后构建 $ V_0=h\times S_0 - p_0 $
  3. 然后用 $ V_1^d=h\times S_1^d+p_1^d $ 算出 V1，用V0一除得到收益率
  4. 注意，看涨期权的V是S-c，看跌期权的V是S+p

风险中性

risk neutrality。

$$ c_0=\frac{\pi c_1^u+(1-\pi) c_1^d}{(1+r)^T}\\ \pi=\frac{1+r-R^d}{R^u-R^d} $$

$ \pi $ 就是risk-neutral probability；或者说是对于价格上升到 $ S_1^u $ 的风险中性概率。

可见，期权价格只需要考虑 $ R^u 和 R^d $ ，也就是volatility。这个价格是不考虑投资者对于风险的偏好的。

无论是call还是put， $ \pi $ 都是一样的。

Tag: 考前看看题熟悉一下。

目录