构建投资组合时最重要的因素是正在考察的单个资产的风险和回报。
Expected return是想要赚取的回报:
rF是无风险收益率; $ \pi $ 是通胀; RP是risk premium。
普遍假设长期(虽然不知道需要多久)的历史平均回报(historical mean return)跟预期回报是相等的。
只用平均值(期望收益)和方差(风险)来评判投资机会的时候,我们假设了1)回报率是正态分布的;2)市场在信息(informationally)和运行(operationally)上都是高效(efficient)的。
(第一点)但是现实里:1)在均值附近是偏的(skewed),不是对称的;2)极端事件发生的概率比正态分布预期的多(肥尾)。
从历史上看,美国大公司股票的收益率是负偏度的。
(第二点)operational limitations的典型是流动性(liquidity)。交易成本有三个组成部分:1)佣金(brokerage commission);2)买卖价差(bid-ask spreads);3)price impact。流动性会影响后两者。
price impact的解释:买100股对价格影响微乎其微;买10000股可能就不一样了。
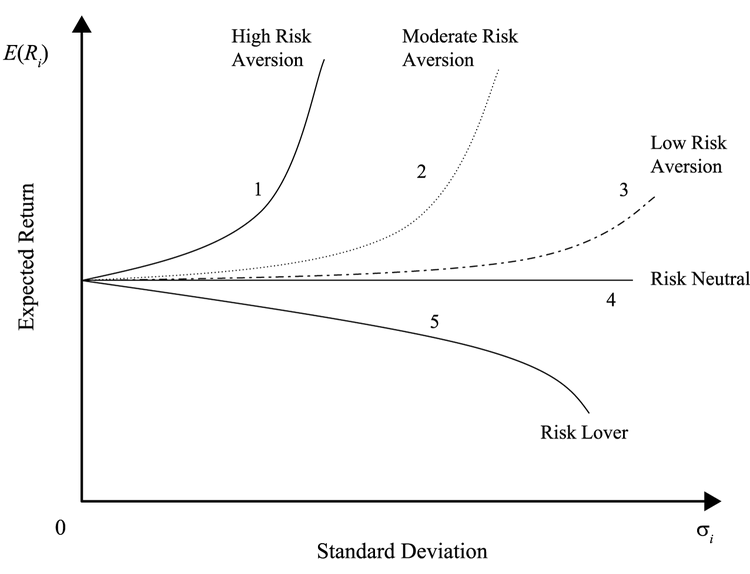
投资者风险偏好
risk seeking风险偏好。即使期望值低于确定的收益,也可能会接受。
risk neutral 风险中性。只关注回报,不关心风险——如果回报更高,风险高一点没问题。如果投资的金额只占财富的一小部分,很多投资者都会表现出风险中性。
risk aversion风险厌恶。即使确定的收益低于有风险收益的期望值,也会接受。在相同的回报下最小化风险,并在相同的风险下最大化回报
风险和回报的关系(历史数据)反映出市场价格是根据风险厌恶者的交易来确定的。投资行业的统一意见是把投资者假设为风险厌恶。
risk tolerance 风险承受能力是指投资者为实现投资目标所能承受的风险程度。
效用理论
注意,按计算器的时候先算后面的再加收益率,不然会被坑。
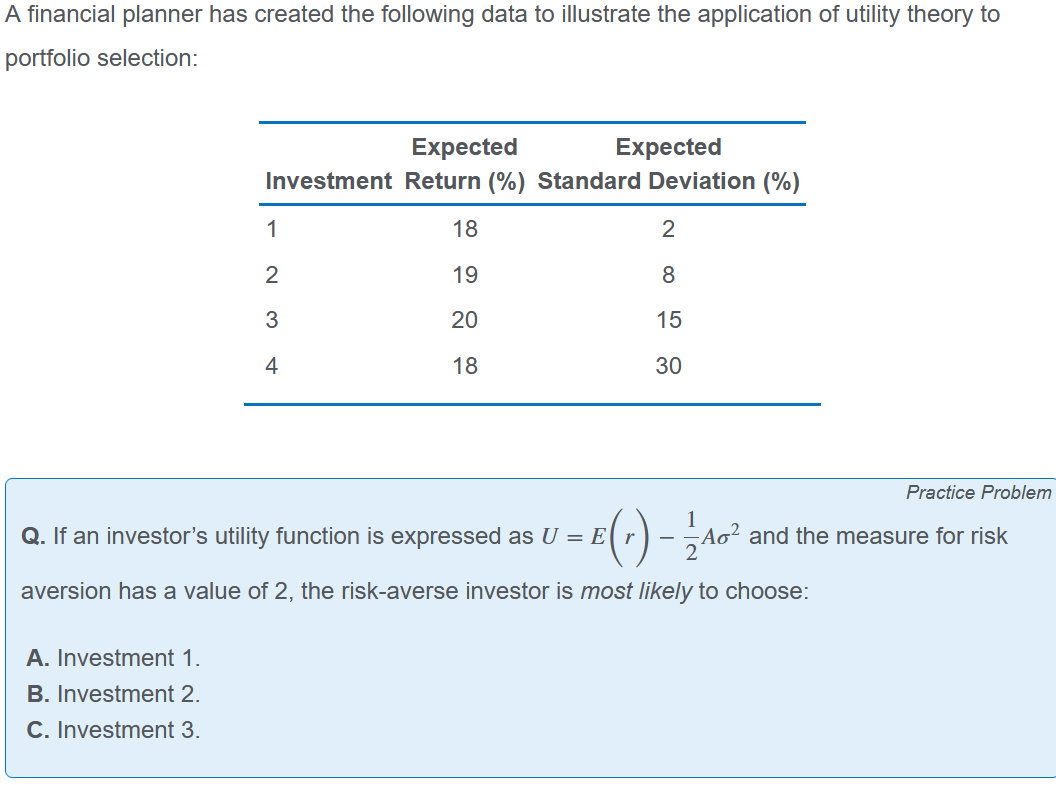
存在几个假设:1)风险厌恶;2)同等风险下最大化收益;3)对投资组合的排序具有一致性(X>Y>Z则X一定大于Z)
A是风险厌恶程度的指标,是投资者接受additional risk所要求的marginal reward。
效用函数的数值只对于ranking有意义。不同个人之间的效用不能比较、求和。
方差会被风险厌恶程度放大。厌恶则A大于0;中性A=0;偏好A小于0。无风险资产由于方差为0,对所有人的效用是相同的。
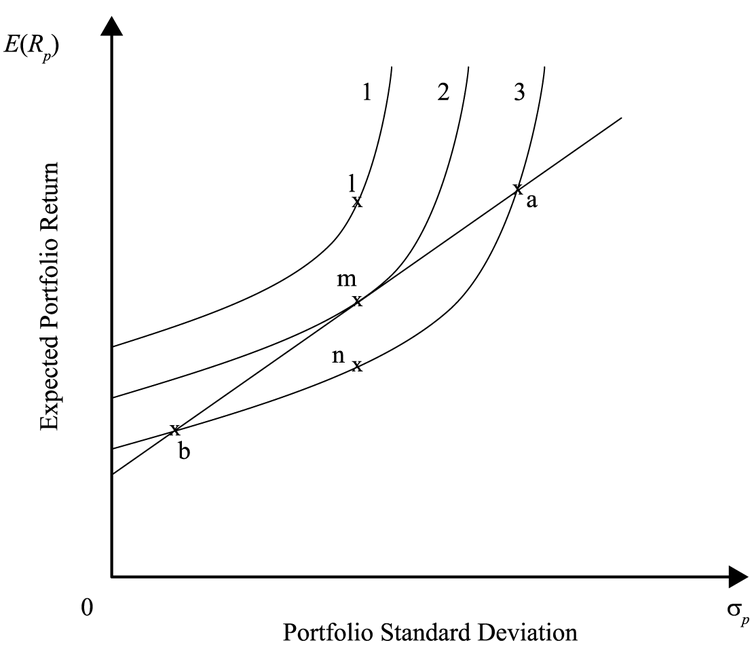
无差异曲线 Indifference Curves
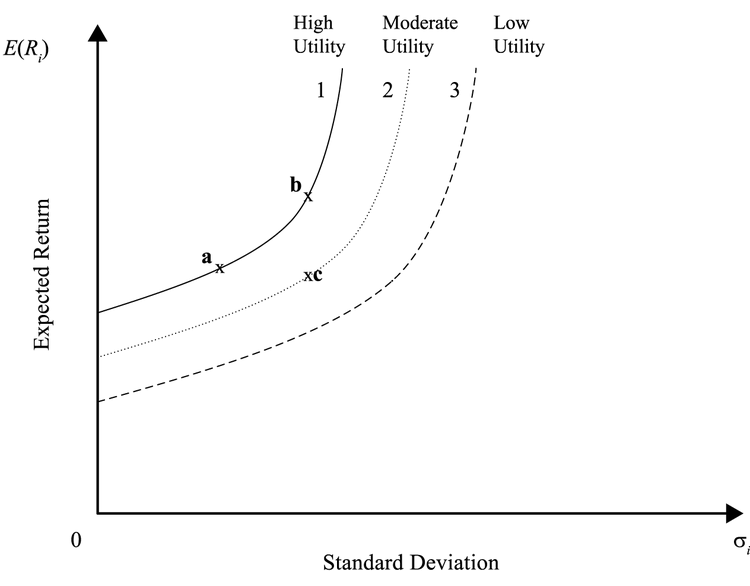
同一条曲线上的任一组合对于同一个投资者来说都是没有差别的。
无差异曲线是弯的,因为边际效用递减(diminishing marginal utility of return):随着风险增加,投资者要求的回报增加的速度加快。弯得越厉害代表着风险厌恶程度越高(A越大)。
资产组合
将一个无风险资产和有风险资产组合起来。
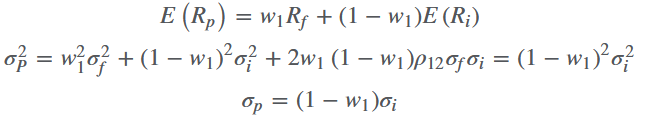
将 $ \sigma $ 变换一下: $ w_1 = 1-\frac{\sigma_p}{\sigma_i} $ ,代入第一条式,得到:
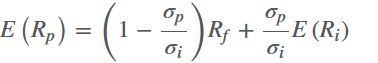
搞一搞:
这就是资本配置线(capital allocation line)。假设市场上只有这两种产品可以选。资本配置线以下的点也是可行的,不过因为相同风险下配置线上的点收益更高,所以投资者会选择上的点;配置线以上(above)的点是无法实现的。
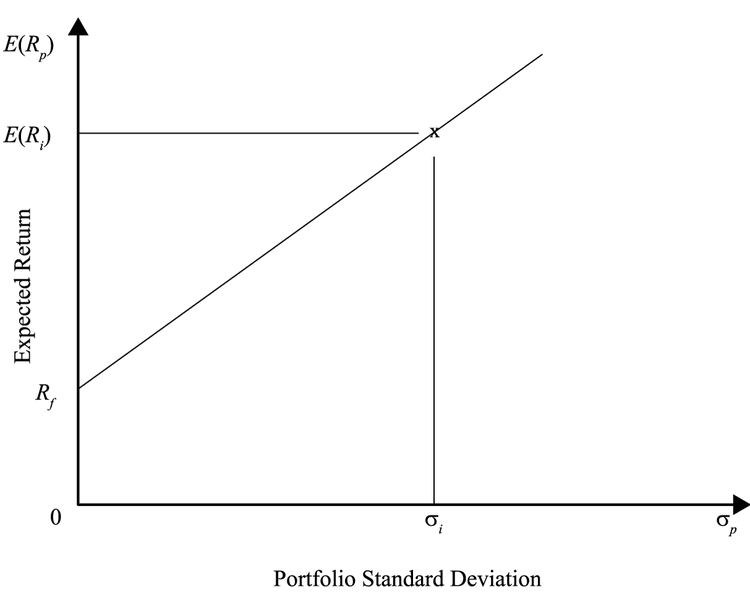
斜率代表着每一单位增加的风险所要求的额外回报,又称风险的市场价格(market price of risk)。
最左边的点是100%投资无风险资产;最右边则是100%投资风险资产。
$ w_i $ 甚至可以是负的,代表着按无风险收益率借入资金来投资风险资产。
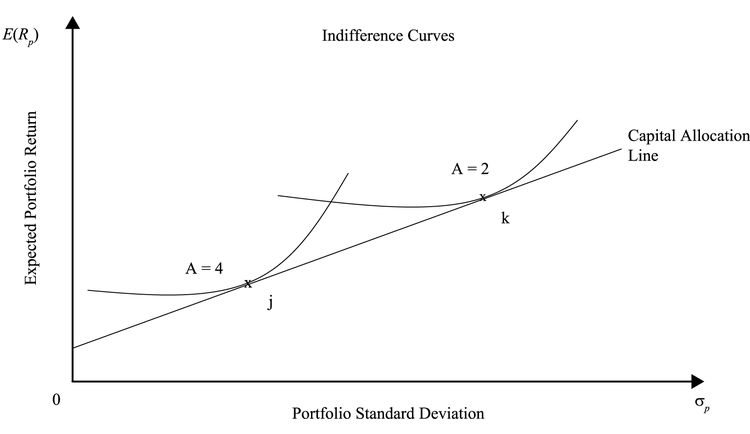
将无差异曲线和资本配置线组合起来就能够得到:
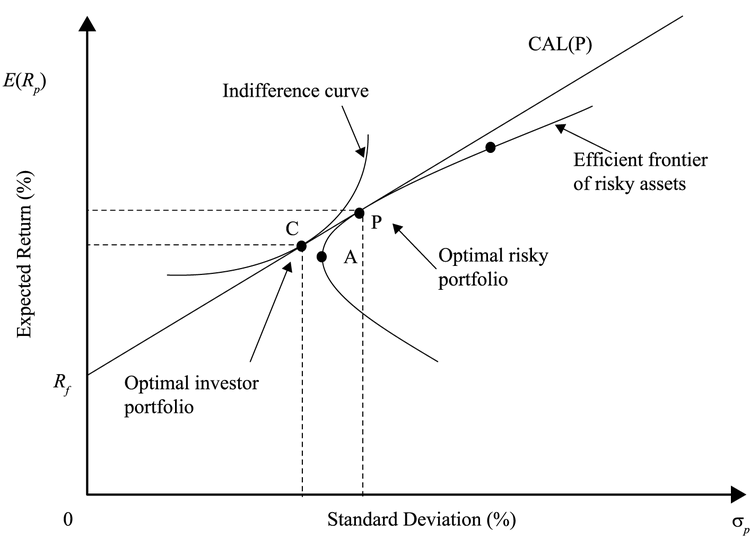
投资者应该选择与资本配置线相切的无差异曲线的那个点所代表的资产组合来实现收益和效用最大化。
投资组合与风险
投资组合的回报(portfolio return)是成分资产的回报的加权平均和:
这是单期回报,没有现金进出,资产组合权重不变。
组合的风险(portfolio risk)则涉及到相关性:
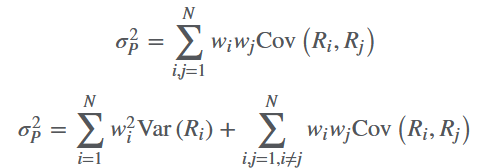
假设两种资产的收益率的correlation是 $ \rho_{ij} $ ,那么 $ Cov(R_i,R_j) = \rho_{1,2}\sigma_1\sigma_2 $ ,有:
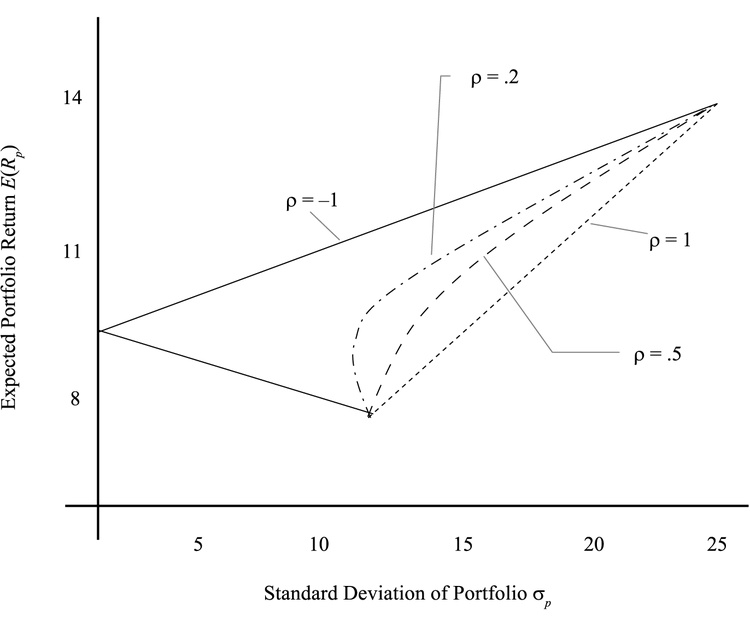
如果 $ \rho = 1 $ ,那么它们的风险对于组合的风险就是直接的加权平均而已,没有导致风险减少; $ \rho < 1 $ 时,显然风险会小于前一种情况。
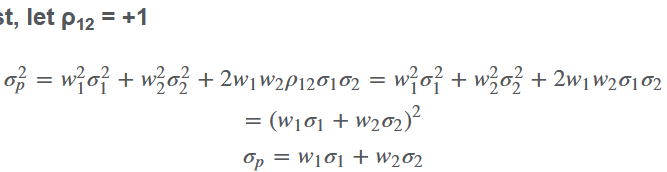
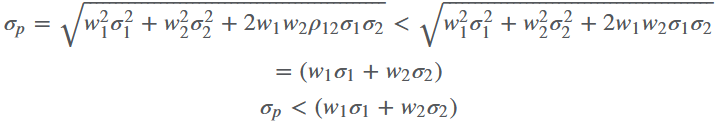
极端情况下( $ \rho = -1 $ ),组合就会无风险。
国内资产与国外资产组合
如果投资组合里面,一个是国内资产,另一个是国外资产;那么国外资产还需要再拆分,视为两种资产的组合:以国内货币计价的外国资产,以及汇率资产。
汇率需要标示为 国内/国外,因为是要把国外资产换回来国内的货币。
两种资产权重都是100%:
如果要算这个投资组合总的收益率和风险,式子会比较复杂:
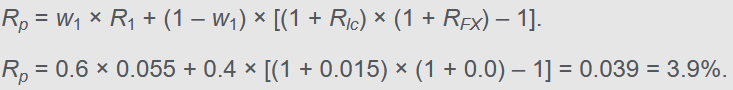
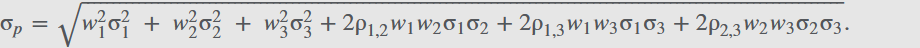
大量资产组成的组合(分散投资)
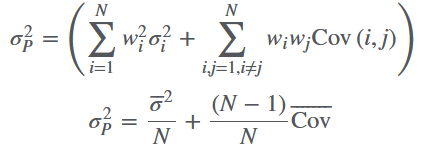
省略推导过程,简单总结:随着N变大,资产之间的协方差会成为风险的主要成分。
高相关性指高于0.9;低相关性指低于0.5。
分散投资(多元化)的方法:
- 资产类别:大类别(比如股票、债券)、中类别(比如大盘股、小盘股、国内股国外股)、小类别(医疗股、能源股)都可以
- 指数基金(index funds):对于小型投资组合来说直接购买股票的成本太高,可以使用指数基金来降低成本。
- 跨国(among countries)
- 不买自己老板的公司的股票:收入是老板发的,代表着组合中的一大部分来自于老板
- 新增资产之间要评估
- 多元化是有成本的:新的资产的交易有成本,追踪一个规模更大的组合也有成本
- 可能是假多元化:新的资产可能名字不同,但是所属类别是你已经持有足够的风险暴露的了
- 买保险或看跌期权
- 保险是典型的负相关资产
使用之前的公式来判断新的资产是否值得加入:
根据第二行:如果新的期望收益更高,那么就可以加;根据第三行:如果新的夏普比率比旧的乘以相关系数(correlation)高,那么就值得加
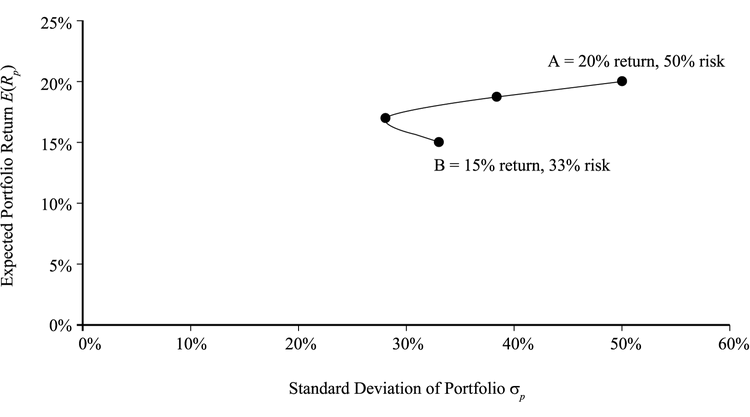
Investment Opportunity Set
投资机会有一个边界(frontier),边界右边的点都是可以通过可用的资产组合得到的。
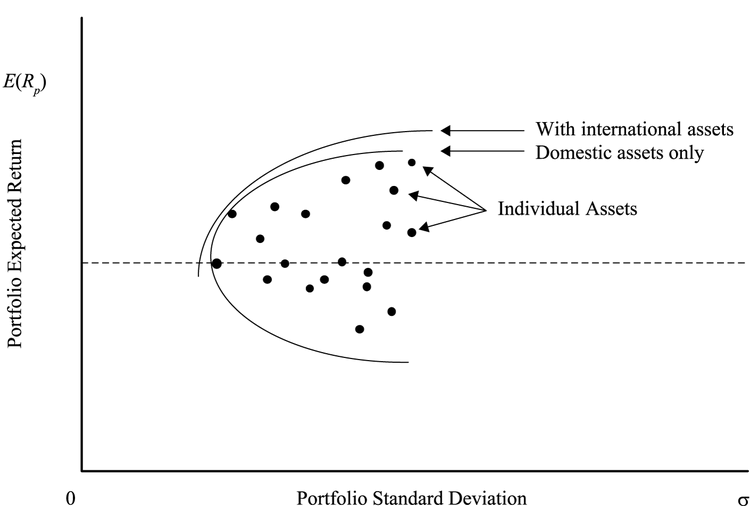
如果新增的资产的类别与现有资产不完全相关,那么边界就会往左上角移动。
注意这里是不包括无风险资产的,所有资产都是有风险的。
最小方差边界
假设以下边界就是最终的边界,已经没有办法通过添加资产来让它继续移动了。
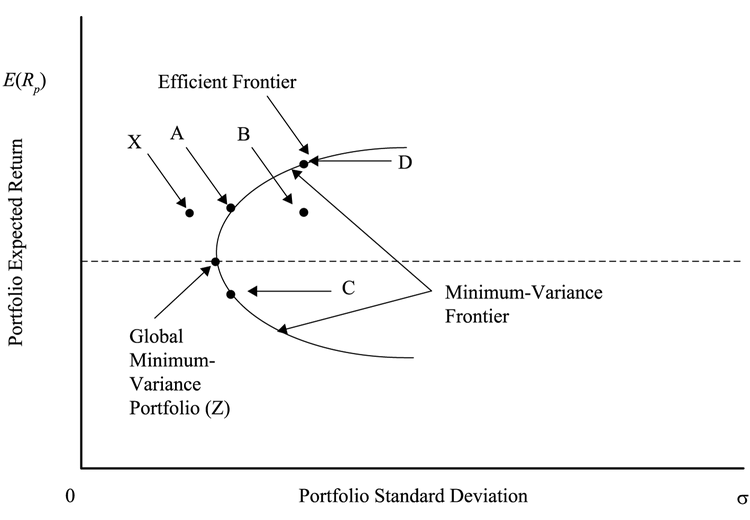
minimum-variance protfolio就是上图中的曲线上的点。风险厌恶的投资者都会选择最小方差边界上的点,因为左侧虽然风险更小但是不可实现;右侧相同收益但是风险更大。
曲线上方差最小的点就是global minimum-variance portfolio全局最小方差投资组合。
由于相同风险下希望最大化收益,所以global minimum-variance portfolio以下的点都不会有人选(inefficient)。
曲线中,global minimum-variance portfolio上方、右侧的部分叫做Markowitz efficient frontier(马科维茨有效边界),理性的、风险厌恶的投资者都会选择这个边界上的组合。
可以观察到斜率是逐渐减小的,投资者获得的收益增量随着假设的风险增加而递减。
现在加入无风险资产:
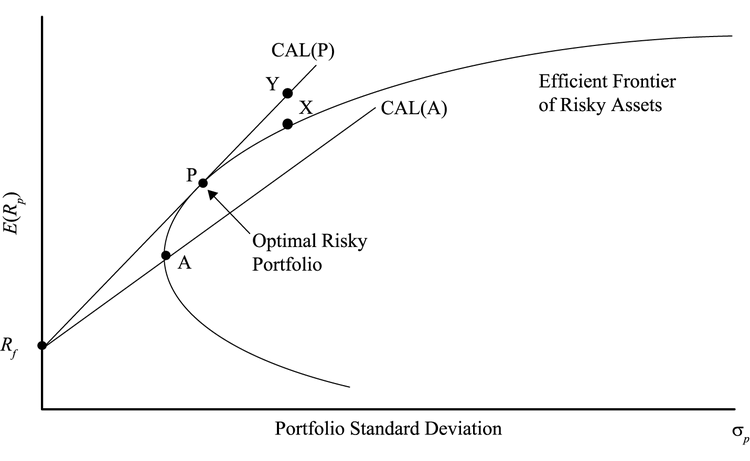
显然配置线P比配置线A更优。
配置线P叫做optimal capital allocation line;资产组合P(P点)叫做optimal risky portfolio。
two-fund separation theorem:所有投资者都会持有由两个portfolio(或基金)组成的组合:1个无风险资产+1个最优风险资产组合。投资问题就分成了两步:
- investment decision:找到最优风险组合(optimal risky portfolio)
- financing decision
这里需要这样理解:确定了最优风险组合之后,结合无风险资产,就确定了资本配置线;但是投资者选择的组合是通过资本配置线和无差异曲线决定的;回忆这个图:

如果投资者选择的点在可行边界上面(比如Y点),那就要借钱(借无风险资产)来投资于最优风险组合;在可行边界下面的,就是把一部分投资于无风险资产。
数学过程:

构建frontier(一般来说自变量都是权重w):
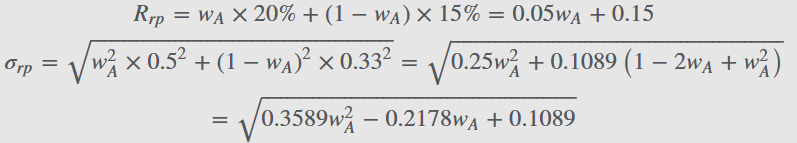
构建资本配置线的一般公式:引入无风险资产,用到公式:

求得斜率的最大值的权重w(用导数,或者题目给出,这里是38.20%),得到与frontier相切的资本配置线:
根据题目给出的风险厌恶系数可以写出效用函数(比如这里是2.5),其中 $ \sigma $ 又从上一条式子算得:
算到效用函数的最大值对应的收益之后,就能得到对应的权重和相应的标准差(风险)
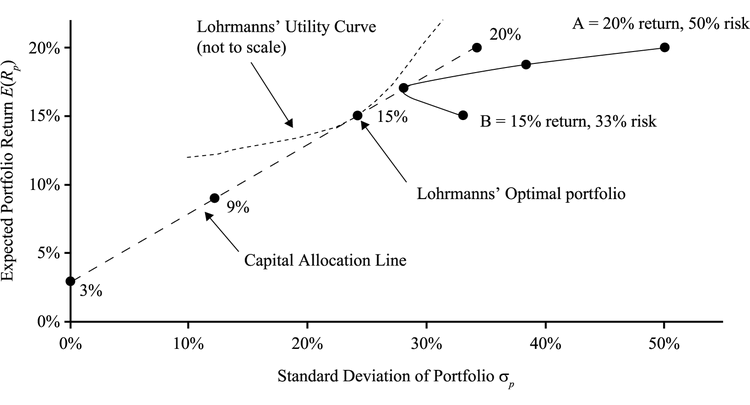
主动和被动投资组合
optimal risky portfolio只有在所有投资者对经济的预期相同时才会唯一,这称作homogeneity of expectations。
如果预期不同,就会得到不同的最优组合。
如果市场是informationally efficient的话,市场价格就是未来现金流折现的无偏估计量(an unbiased estimate of all future discounted cash flows)。被动投资组合(passive portfolios)就是基于这个假设而构建的。
主动投资管理(active investment management)、主动投资组合(active portfolio)则是根据自己的看法判断,对于低估了或者能够提供高于正常的收益的资产设定正权重,其他资产设定0权重甚至负权重。这里的正负是相对于被动投资组合而言的。
资本市场线 CML
Capital Market Line (CML),是资本配置线的一个特例:
- 无风险资产是一个debt security,比如美国国库券
- 风险资产组合是市场组合(market portfolio),比如标普500
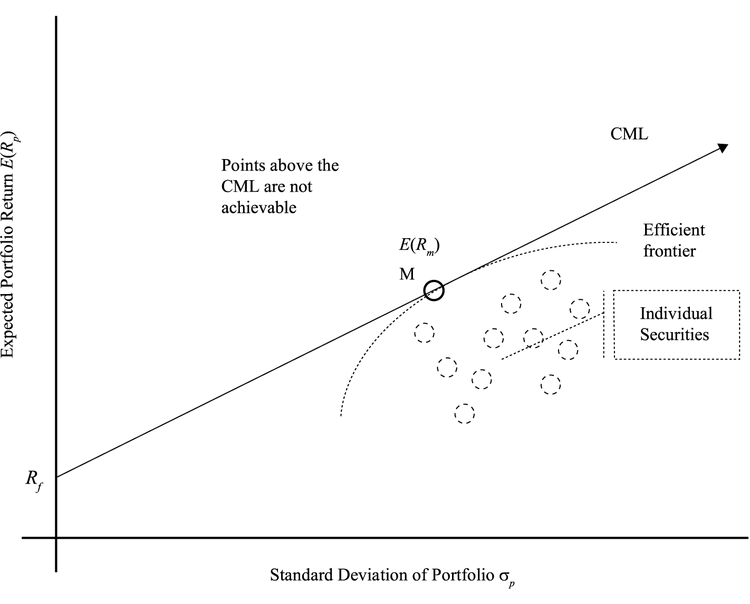
两种风险资产的组合画出来是曲线;而风险资产和无风险资产的组合画出来是直线。
如果选择M点右侧(CML上)的位置,那么被称为“存在无风险资产的负投资(negative investment)”,这部分被称为“风险资产中的杠杆头寸(leveraged position)”。
个人投资者的借款通常高于无风险利率 $ R_f $ ,假设是 $ R_b $ ,那么M点右侧的曲线的斜率就变成了:
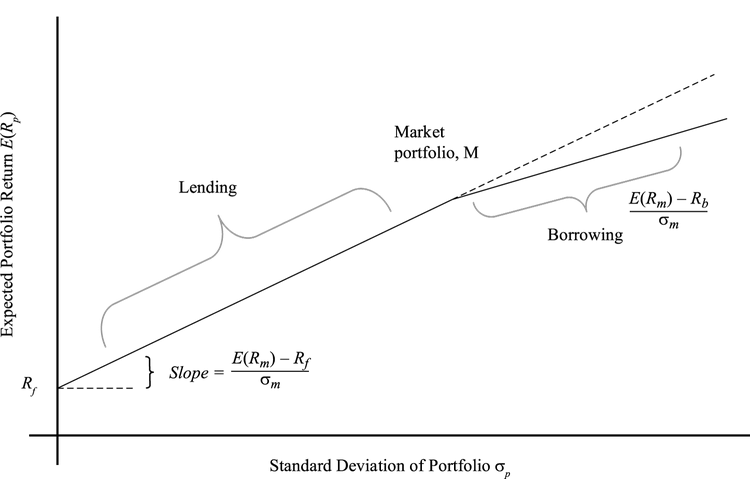
所以CML的公式变成了:
所有被动投资组合都在这种弯曲的CML上。
但是通常计算都会这样算:
系统性风险
Systematic risk,也叫做non-diversifiable/market risk,是影响整个市场或经济的风险;
Nonsystematic risk是与单个公司或行业相关的风险。
系统性风险包括利率、通胀、经济周期、政治、自然灾害等。
总方差=系统性方差+非系统性方差
系统性风险因为无法被分散,所以投资者应该为承担系统性风险得到补偿;相反,非系统性风险因为可以被分散,所以不应该补偿。
无风险资产连系统性风险都没有。market portfolio则是没有非系统性风险。
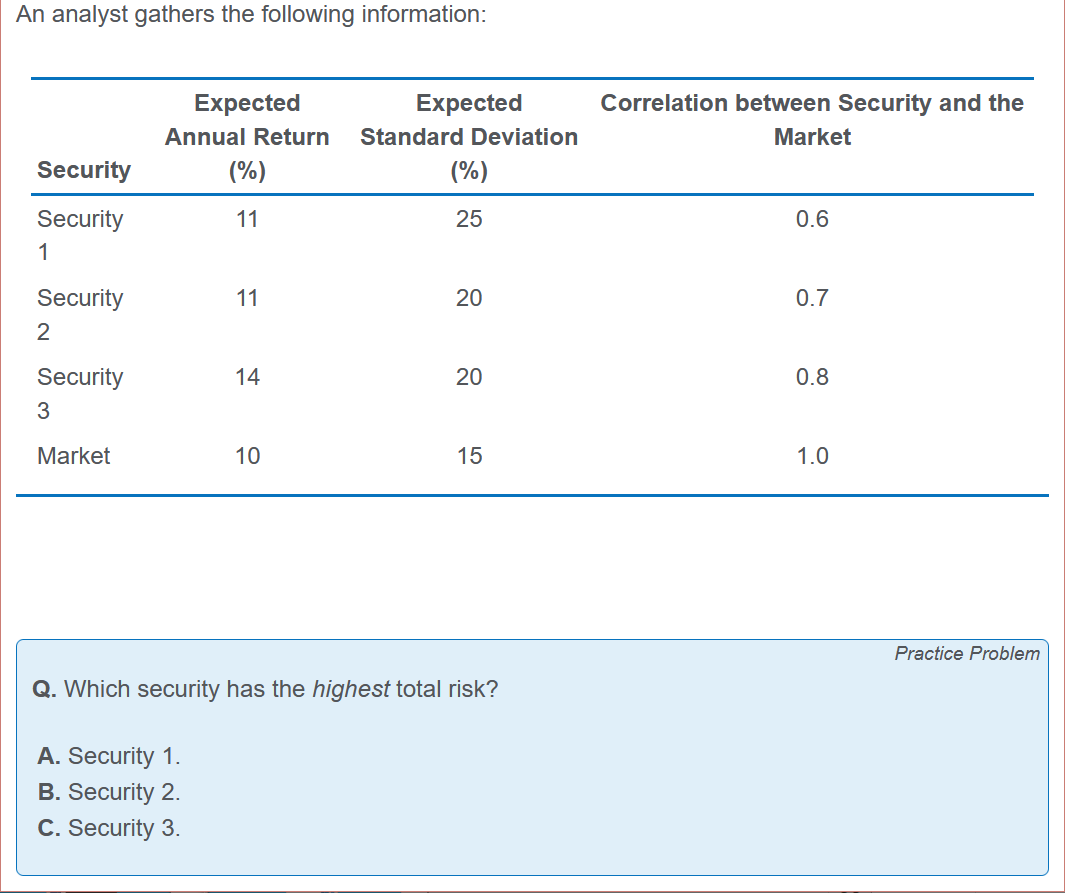
每个证券的 $ \sigma_i $ 就是它的总风险。
回报生成模型
Return-generating model,在给定某些参数的情况下,提供证券(security)的预期回报的模型。如果系统风险是回报的唯一相关参数,那么回报生成模型将在给定系统风险水平的情况下估计任何资产的预期回报。
multi-factor model:
- Macroeconomic factor models:使用与证券回报相关的经济因素。比如利率、通胀率等
- Fundamental factor models:使用公司基本面的相关因素。比如收入、现金流
- statistical factor model:分析历史和横截面收益数据,以确定能够解释观察到的收益中方差或协方差的因素。问题是分析出来的因素可能没有经济意义。
通用形式是:
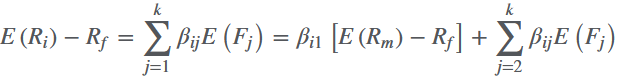
每个因子的权重叫做factor weight(也叫factor loading)。其中market return是单独列出来的,所有模型都将market portfolio的回报作为关键因素。
单因素模型
将CML的式子改一下,就成了单因素模型:
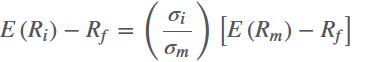
factor loading 是 $ \sigma_i / \sigma_m $ ,表示the ratio of total security risk to total market risk。
接下来的推导都是为了将
$ E(R_i) - R_f = \frac{\sigma_i}{\sigma_m}[E(R_m)-R_f] $
变成
$ E(R_i) - R_f = \beta_i[E(R_m)-R_f] $
来证明CML就是一个单因素模型。
将式子中expected return改为realized return;realized和expected之间的差值来自于非市场变动(non-market changes),标记为 $ e_i $ :
那么realized return的方差就是:
这就体现出了“总方差=系统性方差+非系统性方差”。又因为CML代表的market porfolio已经完全分散了,所以没有非系统性方差;所以 $ \sigma_i = \beta_i\sigma_m $ 。得证,CML就是一个单因素模型。
市场模型
Market model,通常被用来测量beta风险和计算abnormal returns。市场模型是一个单因素模型,只有market return这个factor:
其实来自于这条:
beta和alpha都用历史数据来estimate。
比如回归测得沃尔玛对标普500的alpha是0.0001,beta是0.9,那么沃尔玛的expected daily return = $ 0.0001 + 0.90 × R_m $
abnormal return:如果市场升了1%而沃尔玛升了2%,那么:
$ e_i = R_i-E(R_i)=0.02-(0.0001+0.9\times 0.01)=0.0109 $
即沃尔玛那一天的非正常回报是1.09%。
计算beta
系统性风险是 $ Cov(R_i,R_m) $ 。因为无风险利率是常数,没有方差,所以(再次提到,e是non-market return,和market return的协方差是0):
所以计算beta有两种:
- 要么给出协方差和市场的标准差
- 要么给出市场与资产的correlation和各自的标准差
正的beta代表资产回报与市场方向相同;负的就是相反。无风险资产的beta是0(因为协方差是0)。市场的beta是1。
当然最实际的方法还是用历史的Ri和Rm来回归。
更短周期的(12个月)的beta更加能反映当前的系统性风险,但是也更容易被特殊时间干扰;更长周期的beta更加准确,但是未来太远了。
CAPM
CAPM这么写:
$ E(R_i) = R_f+\beta_i[E(R_m)-R_f] $
影响回报的首要因素就是beta。如果资产要求的回报率低于无风险利率(beta小于0),那么它加入到组合里能够降低风险。比如保险。
CAPM假设资产的预期收益只因为系统性风险而改变。只要beta相同,任何资产无论性质如何它们的收益都会相同。
CAPM的假设:
- 投资者都是风险厌恶的、效用最大化的、理性个体
- 只要是风险厌恶就行,没有规定程度
- 效用最大化就是总是想要更多的财富
- 理性可以有一部分不理性,只要理性的投资行为占主导或者非理性的对冲掉就行
- 市场无摩擦(没有交易成本和税收)
- 特别是可以以无风险利率借贷
- 卖空成本和卖空限制比起其他要求,影响更严重导致资产价格上行
- 投资者是按照相同的单持有周期做计划的
- 投资者预期是同质的
- 核心是所有投资者都有相同的optimal risky porfolio
- 所有资产都可以无限细分(infinitely divisible)
- 投资者是价格接受者
SML
证券市场线Security Market Line。截距是 $ R_f $ ,斜率是 $ R_m-R_f $ 。
SML的斜率反映的是市场风险。
与CML不同,SML对于任意资产(无论efficient)都能用。
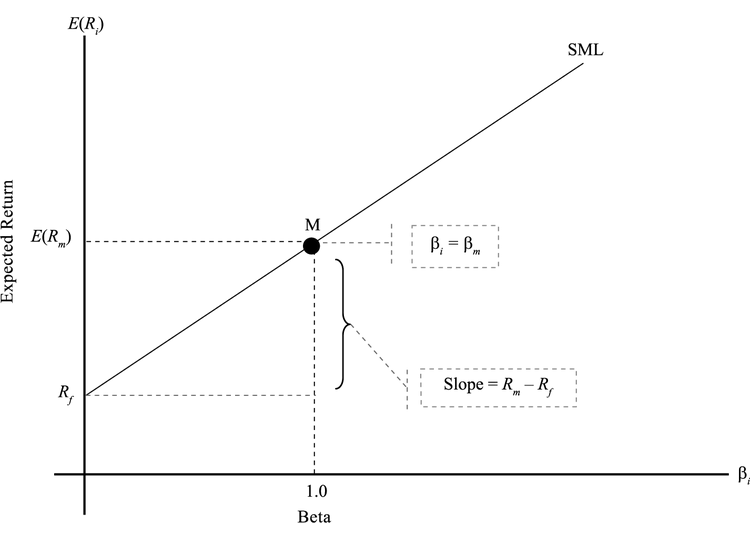
如果有多个资产,有多个beta,那么portfolio的beta就是它们的加权平均值。以两个资产为例:
可以用CAPM来计算某个项目计算NPV的时候所需要用到的required return rate。
总而言之就是用CAPM算出来的预期回报在这种情况下用作NPV的discount rate

局限性
理论局限性:
- 是单因素模型
- 是单周期模型:可能导致短视(myopic)或者是次优选择
实践局限性:
- market portfolio要求包括所有资产类型(甚至包括不可投资的)
- 没有true市场组合的情况下只能使用proxy,但是根据本地条件不同的分析师会使用不同的proxy,这又违反了同质性假设
- 对beta的估计
- 需要使用长时间的数据来估计beta,但是这些数据不一定反映了当下的情况
- 使用不同时间的数据会导致beta不同——同一个资产只是因为使用的数据时间不同就有了不同的return
- CAPM的预测的实证检验很差
- 投资者的期望不是同质的
其他模型
理论上套利定价模型(APT)比CAPm好,但是从实践上CAPM更被偏爱。
实证方面,四因素模型(four-factor model)。
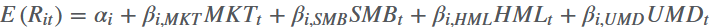
MKT是市场投资组合的超额收益;SMB是小盘股与大盘股的回报率差异;HML是高账面市值比股票和低账面市值比股票之间的回报率差异;UMD是上一年赢家和输家的回报差异;左侧是资产回报中超过一个月国库券回报的部分。实证检验中MKT的系数与0没有显著差异。
资产组合表现评估
Portfolio performance appraisal measures。performance evaluation分为:
- 过去表现如何?未来表现会如何?(performance measurement)
- 怎么产出过去的表现的?未来表现的来源是什么?(performance attribution)
- 是因为技能还是运气?(performance appraisal)
夏普比率
Sharpe Ratio,
夏普比率也可以用realized(historical)data来算。
夏普比率有两个limitation:1)用的是total risk,但是只有systematic risk是priced的;2)需要在比较中才能显示优劣,单独一个没有传达什么信息。
特雷诺比率
Treynor ratio。是为了解决夏普比率的第一个limitation,把 $ \sigma $ 改用 $ \beta $ 了。
limitation是beta也不能为负。
M平方
$ M^2 $ (risk-adjusted performance,RAP):
$ M^2 $ alpha 就是这个算出来的值减去市场回报的结果,表明这个组合outperform了market pofolio多少。
Jensen’s alpha
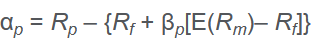
market portfolio的alpha根据定义是0,所以算出来的这个如果是正的就outperform,负的就是underperform。式子里的所有return都是realized return。如果周期长到无风险利率发生了变化,那就用average的。
也是属于回答了“超过了百分之多少”的measure。同时也是你应该接受的支付给manager帮你理财的最高的金额。
选择
如果投资者持有的组合不是完全分散的,那就需要用total risk的那些measure(夏普和M2)
如果是完全分散的,那就只需要考虑系统性风险,那就是T ratio和jensen’s alpha。
如果基准存在错误那么结果也会有误导性(比如用标普500来评估房地产基金)。
CAPM与构建组合
Security Characteristic line
SCL是证券的超额收益相对于market的超额收益( $ R_i-R_f $ 相对于 $ R_m-R_f $)。
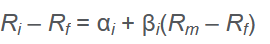
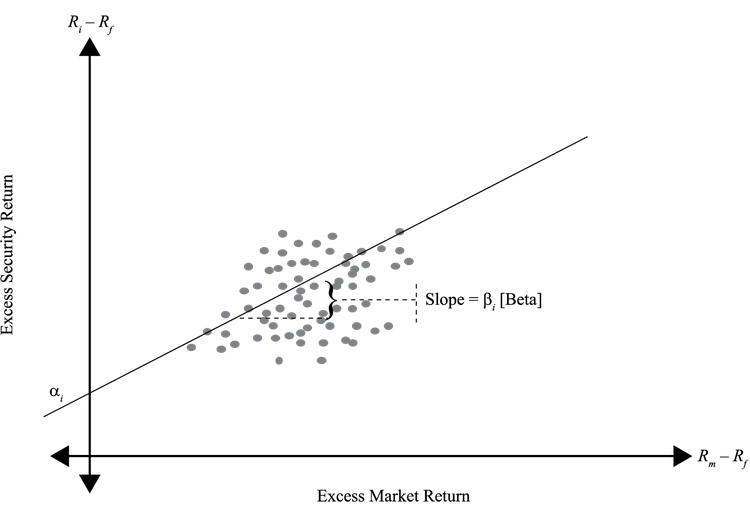
选择证券
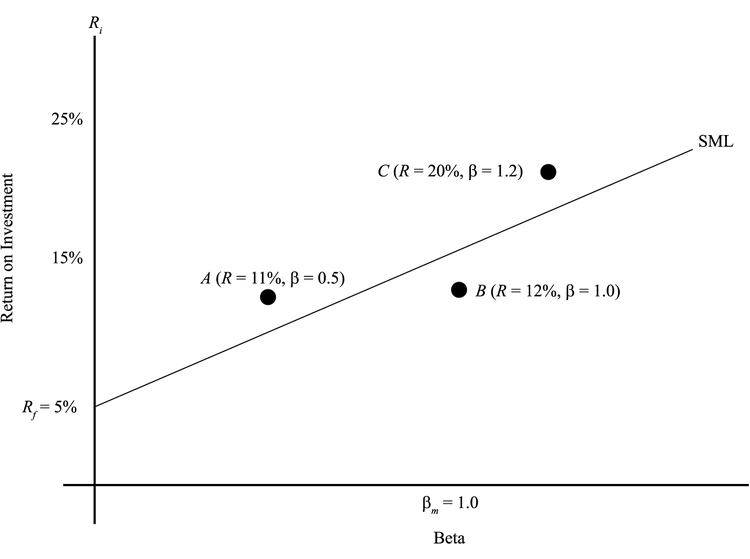
SML上的点反映的是市场的共识定价。以上的点代表着预期回报高于市场定价,是一个好选择;反之。
构建
通过添加来构建一个足够分散的组合(通常来说30个就行,但是需要足够随机)。
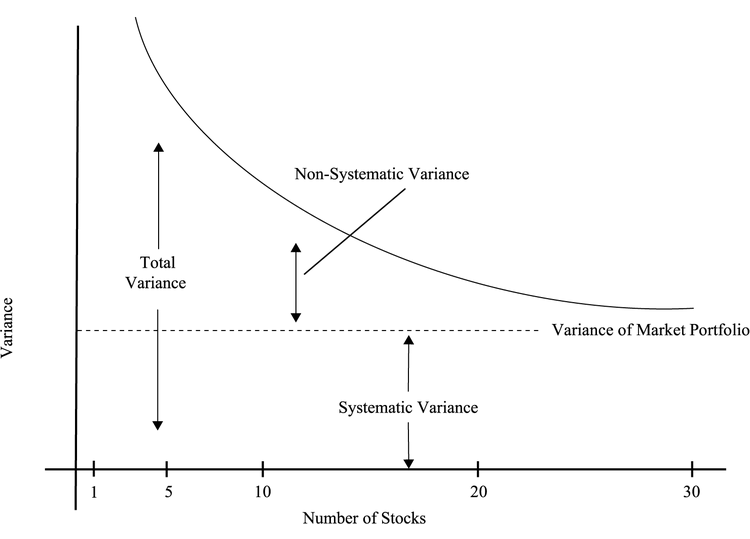
以标普500作为基础来进行构建;任何标普500之外的证券都是潜在目标。根据证券的 $ \alpha_i $ 来是否添加。只需要与标普500的correlation不高而且回报足够补偿它的系统性风险就能够有一个正的alpha。
如果标普500里有高估或低估的股票也应该剔除——总而言之就是减少alpha为负的证券的头寸,增加alpha为正的头寸。
每个标普500之外的证券的权重都应该与 $ \frac{\alpha_i}{\sigma_{ei}^2} $ 成比例;整体权重应该与 $ \frac{\Sigma{w_i\alpha_i}}{\Sigma{w_i^2\sigma_{ei^2}}} $ 成比例。
informational ratio: $ \frac{\alpha_i}{\sigma_{ei}} $ 衡量证券向多元化投资组合添加的每单位风险的abnormal回报。越大越好。
$ \sigma_{ei} $ 是非系统性风险。