归类方式:
- numerical 和 categorical
- cross-sectional 和 time-series 和 panel
- structured 和 unstructured
Numerical data 也叫 quantitative data,分成 continuous 和 discrete 两种。
Categorical data 也叫 qualitative data,通常来说各取值之间是 mutually exclusive 的;又根据取值能否进行rank或排列分成 nominal 和 ordinal。但是所有的categorical data都是无法进行有意义的数学运算的。
Cross-sectional data are a list of the observations of a specific variable from multiple observational units at a given point in time. The observational units can be individuals, groups, companies, trading markets, regions, etc.
Time-series data are a sequence of observations for a single observational unit of a specific variable collected over time and at discrete and typically equally spaced intervals of time.
Panel data are a mix of time-series and cross-sectional data.
Structured data are highly organized in a pre-defined manner, usually with repeating patterns. The typical forms of structured data are one-dimensional arrays or two-dimensional data tables.
Unstructured data, in contrast, are data that do not follow any conventionally organized forms. 1 Typically, financial models are able to take only structured data as inputs; therefore, unstructured data must first be transformed into structured data that models can process.
Frequency Distribution
频率分布表。对于categorical数据就直接按分类算次数就可以。对于numerical数据则:
- 算数值range
- 确定bins数量(k)
- 计算每个bin的宽度(range/k),需要向上取整(以便包含最大值);
- 除了最后一个bin,其他都是左闭右开的区间
- 把数值归类到bin里面
Absolute frequency就是频数,relative frequency就是频率。对应的还有cumulative absolute frequency和cumulative relative frequency.
如果出现太多的empty bins,那就说明k太大了,需要减少。
Contingency Table
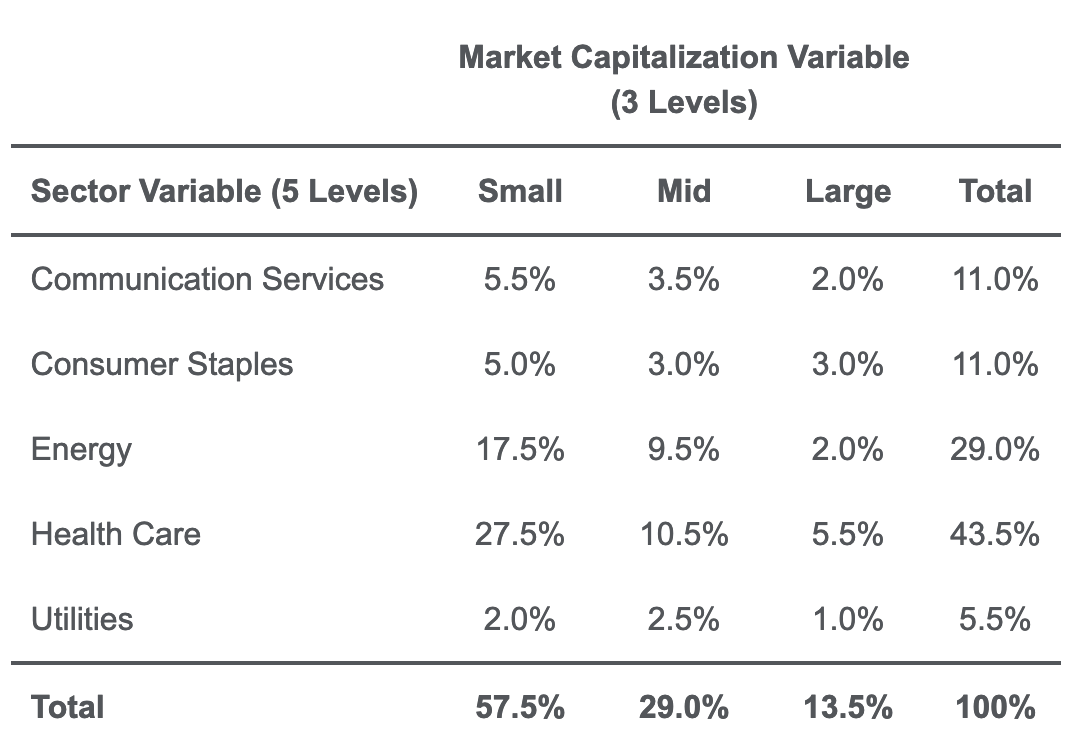
列联表。格子里的数据叫做joint frequencies。行和列的和以及总和叫做marginal frequencies;marginal frequencies展示的就是frequency distribution for each variable。2
用来评估模型performance的时候,就会叫做 confusion matrix 。
Visualization
直方图(Histogram)和 frequency polygon:
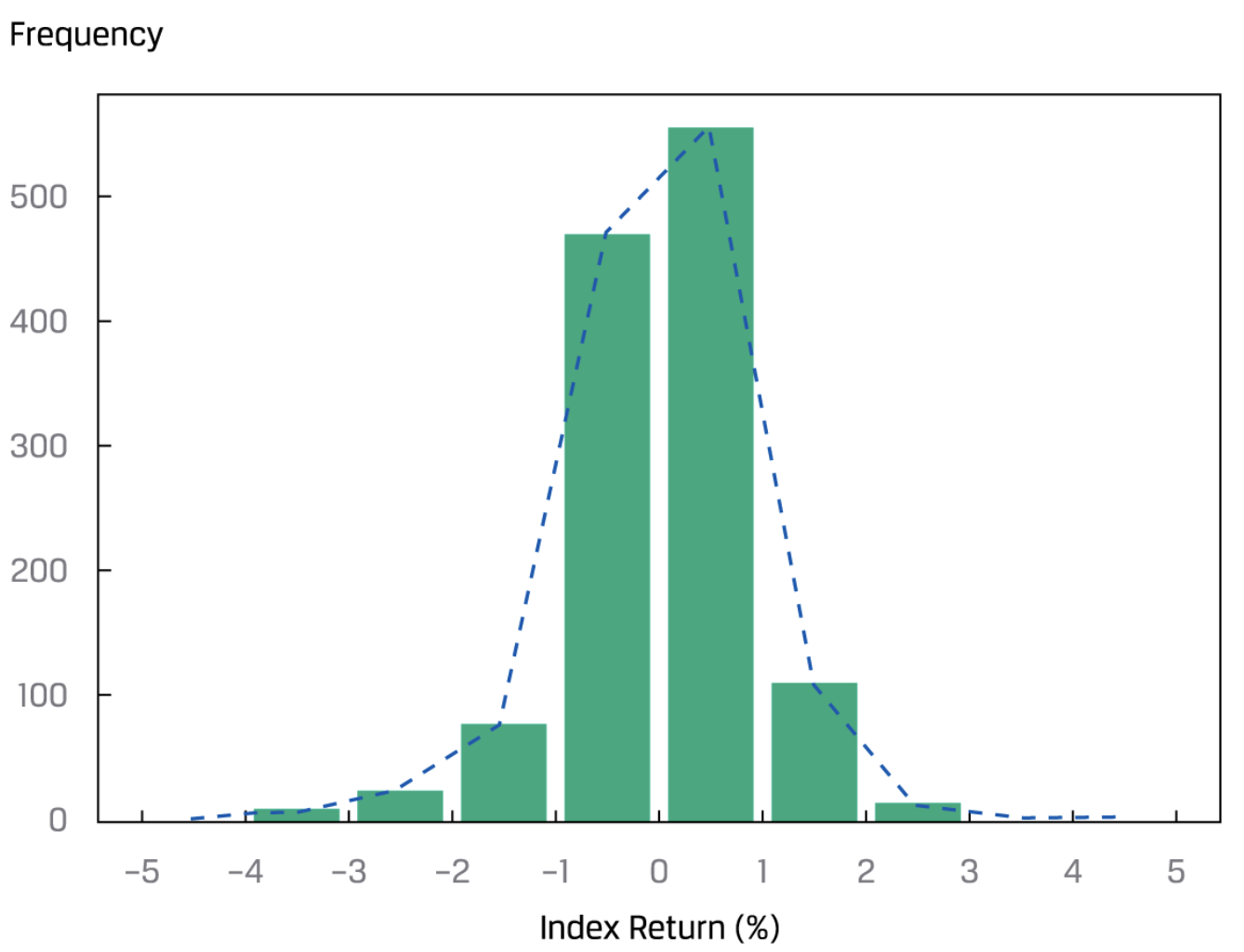
还有cumulative frequency distribution chart,就是累积分布图,用来直观得到某个值以下的observation的数量(或占比):
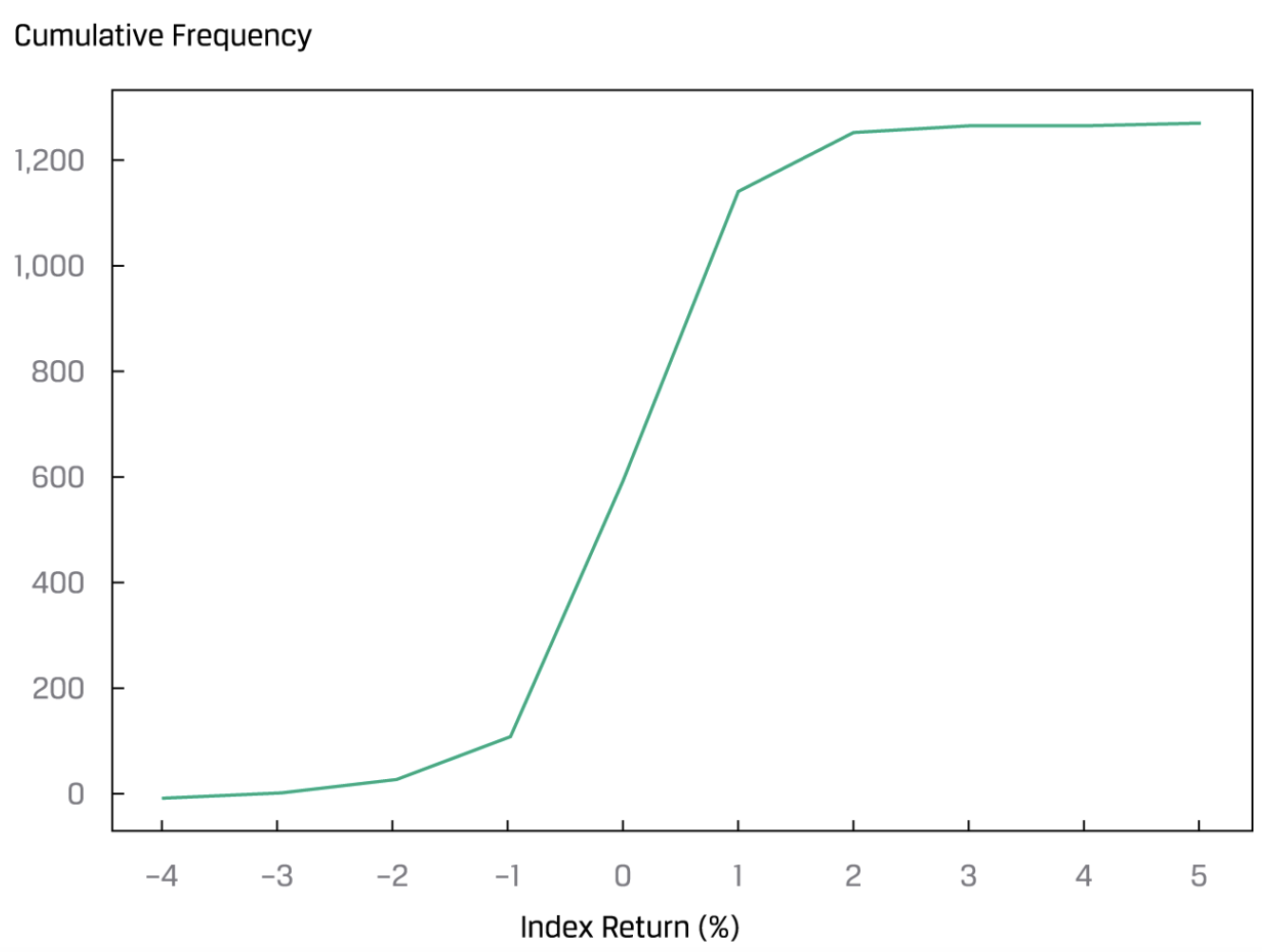
Bar chart则是用来展示categorical数据的;其中还有一种特殊形式叫Pareto Chart,各categories是按照降序排列,而且有一条线display cumulative relative frequency数据。
如果是panel data的话,可以用grouped bar chart(又叫clustered bar chart)或者stacked bar chart来展示:
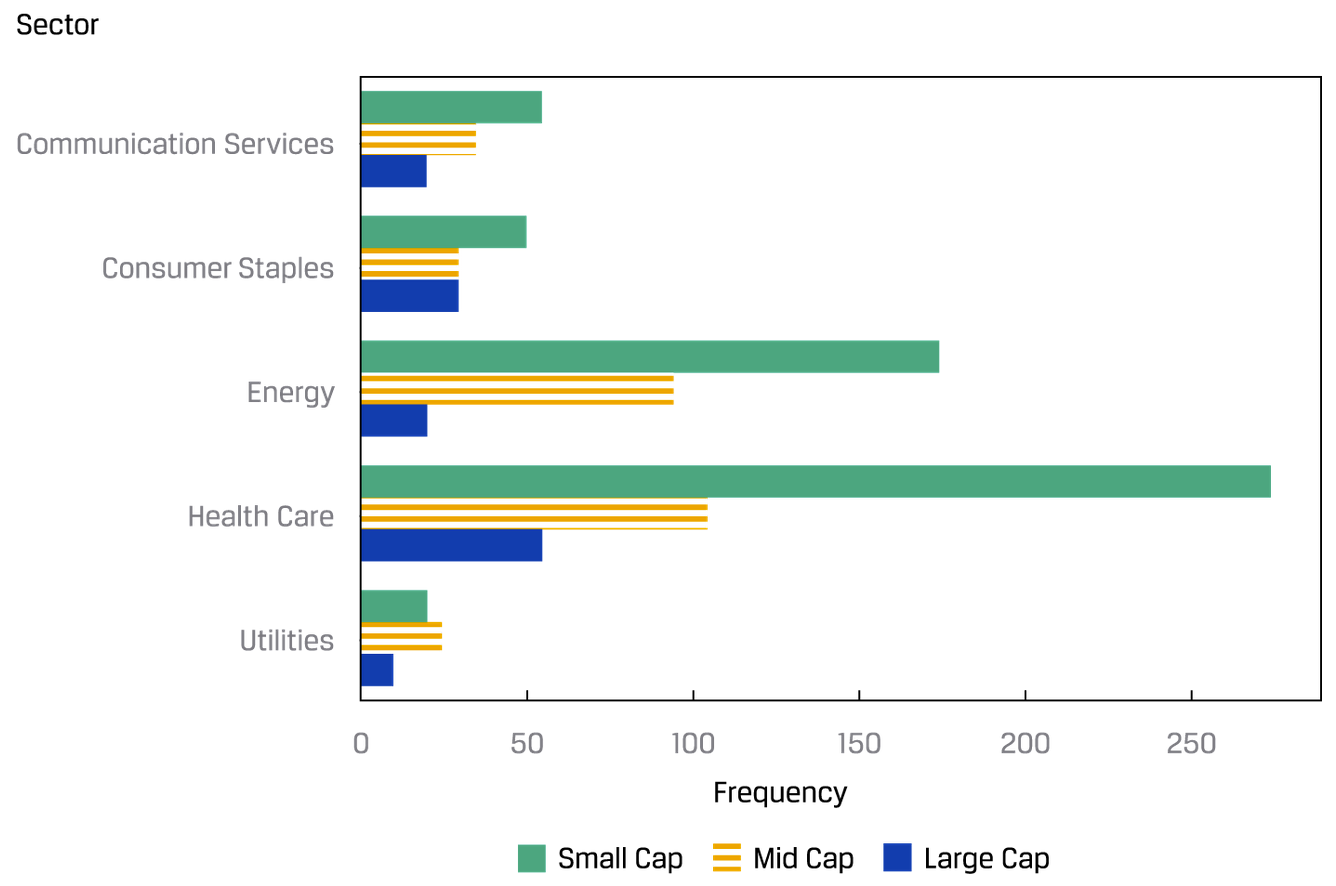
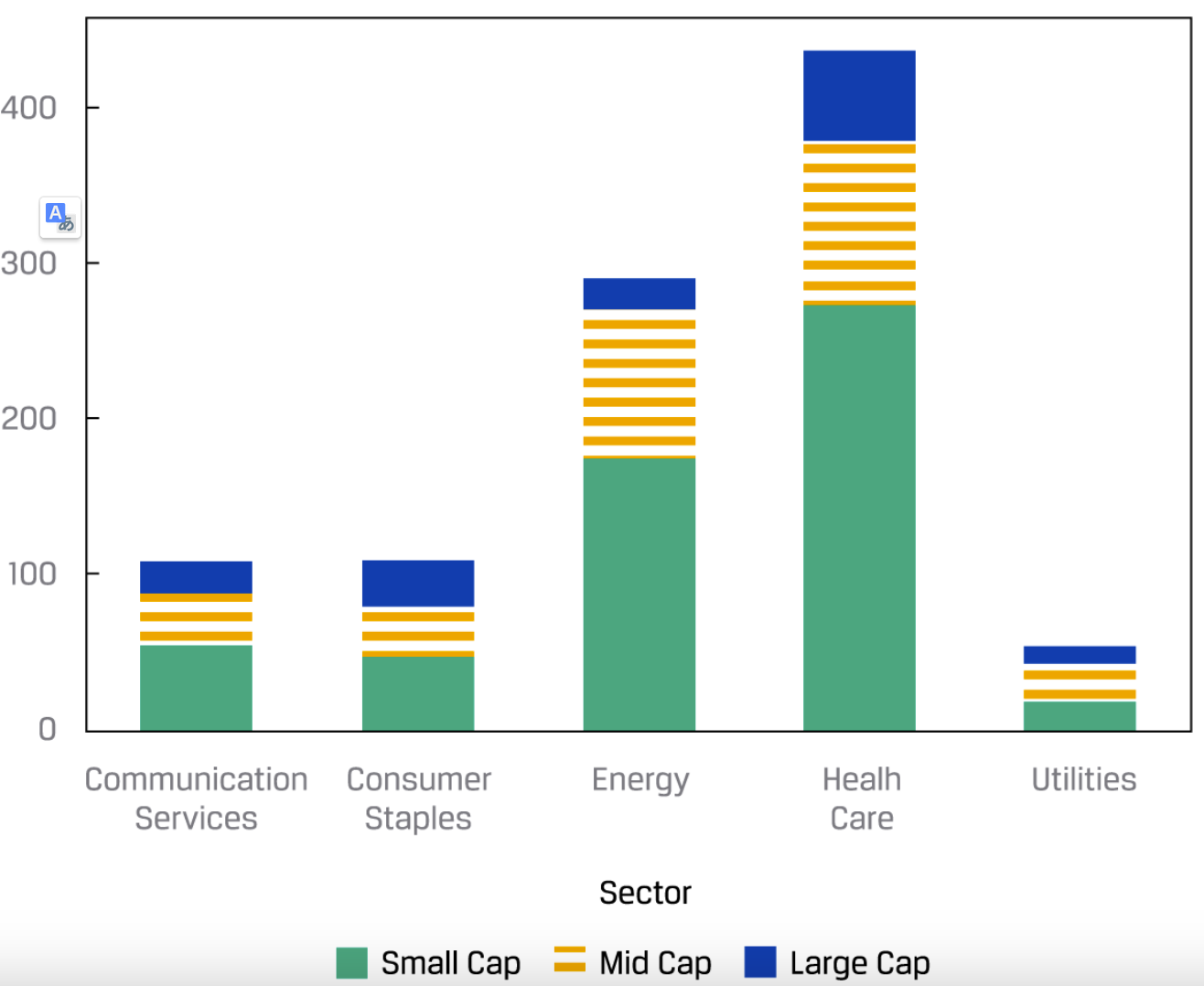
Categorical数据也可以用Tree-Map来展示,但是一般来说数据不会超过3个level:
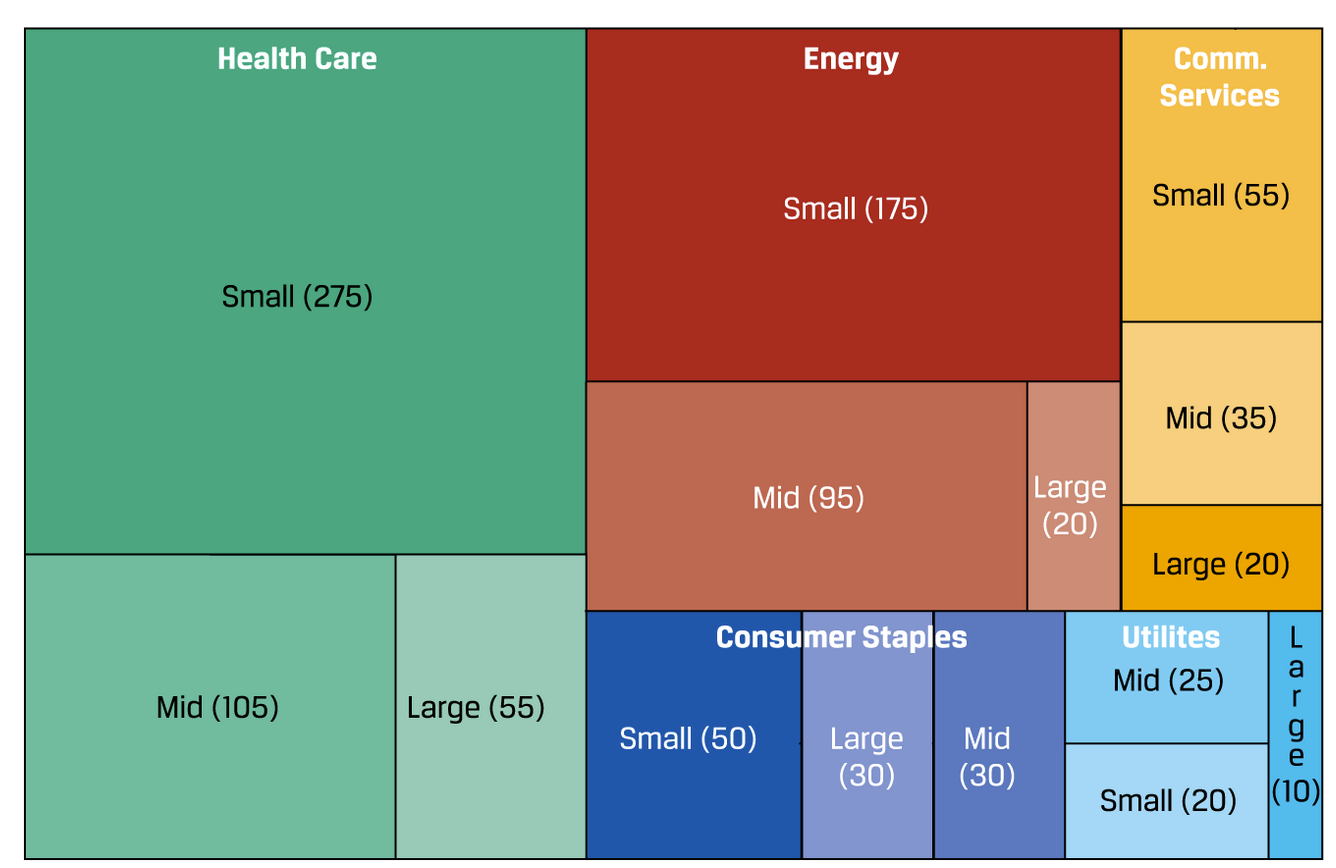
非结构化数据中的文字数据可以用word cloud(或者tag cloud)来展示。
线图(line chart)。当数据超过2项时(左右轴都用上了),如果要展示第三种数据,就要用到bubble line chart:
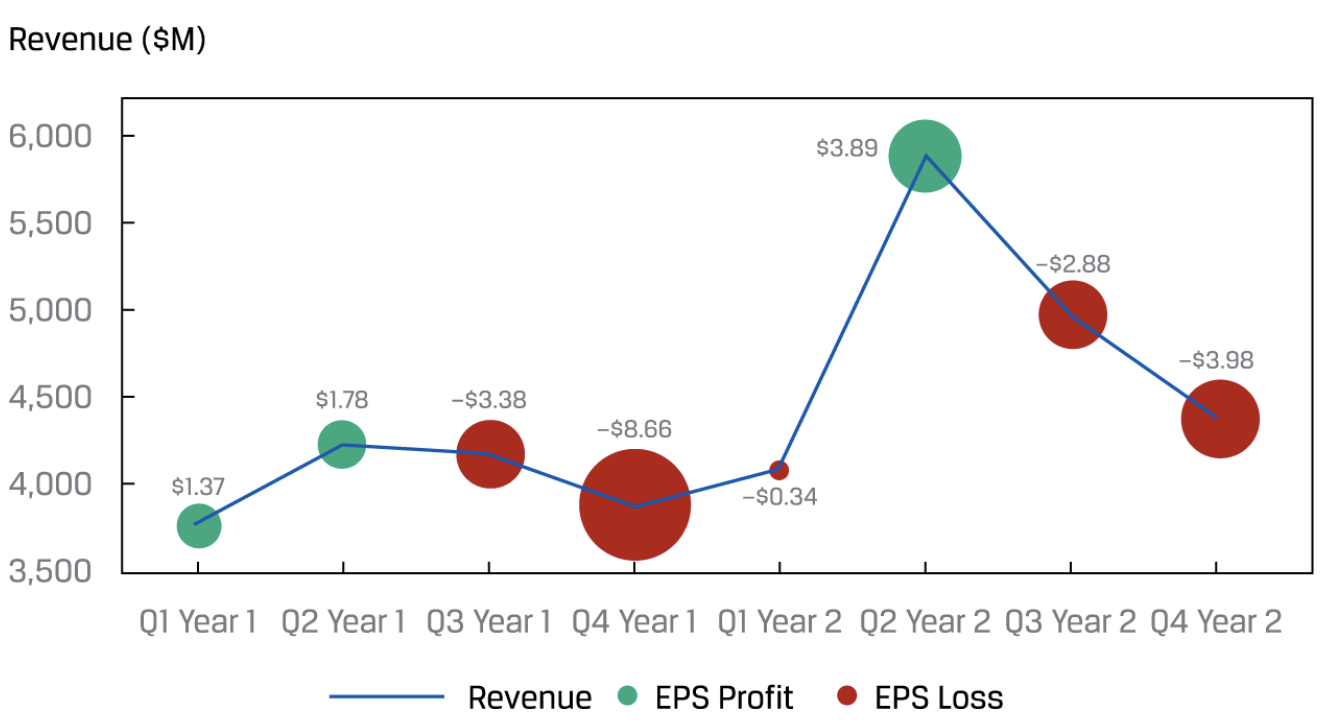
Scatter Plot可以用来初步判断两个变量之间有没有联系、data的range以及极端值(outlier):
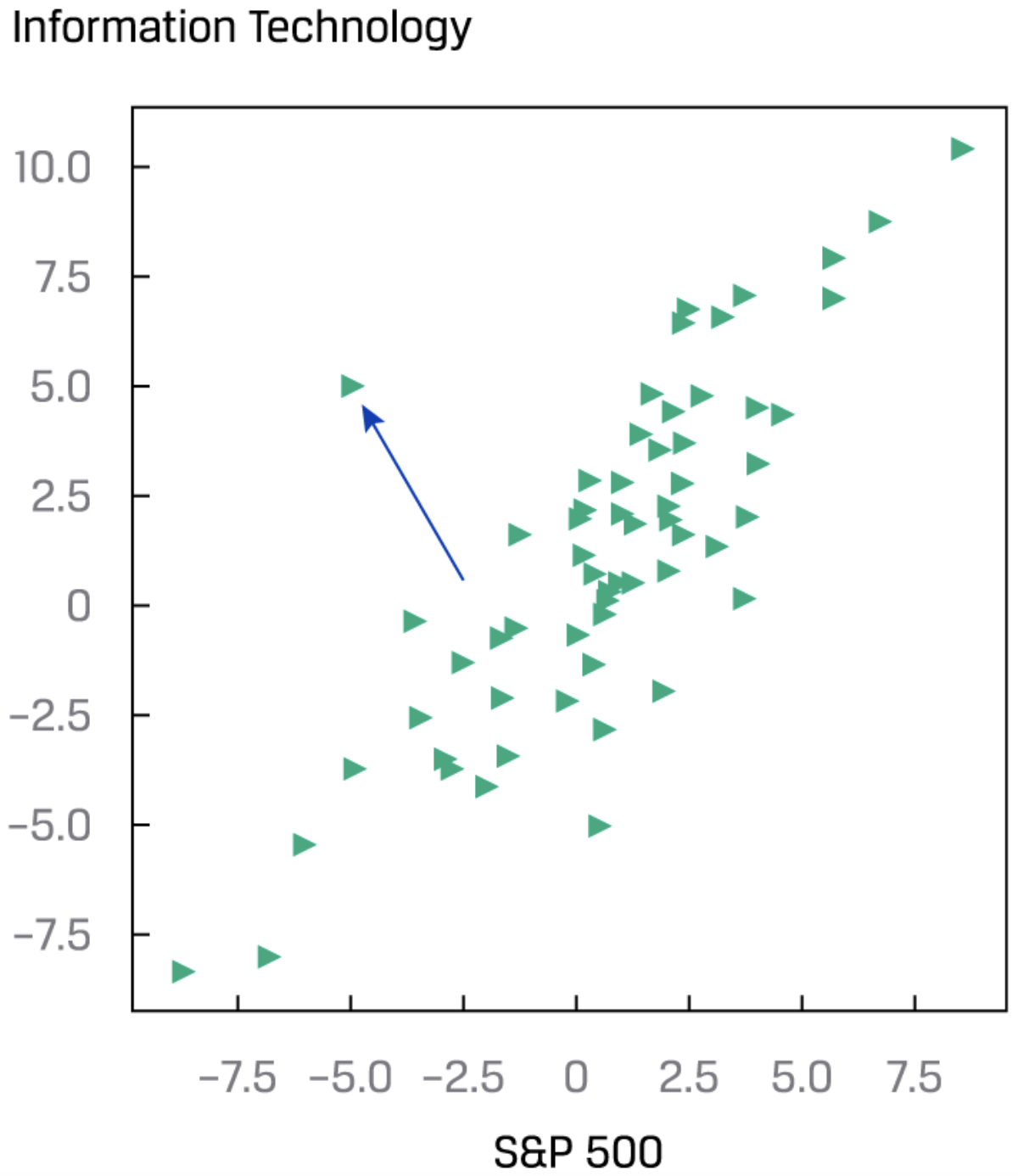
很多个scatter plot组合成的matrix可以提供进一步的分析。
Heat map(感觉就是上色的列联表)。它也可以用来展示不同变量之间的correlation:
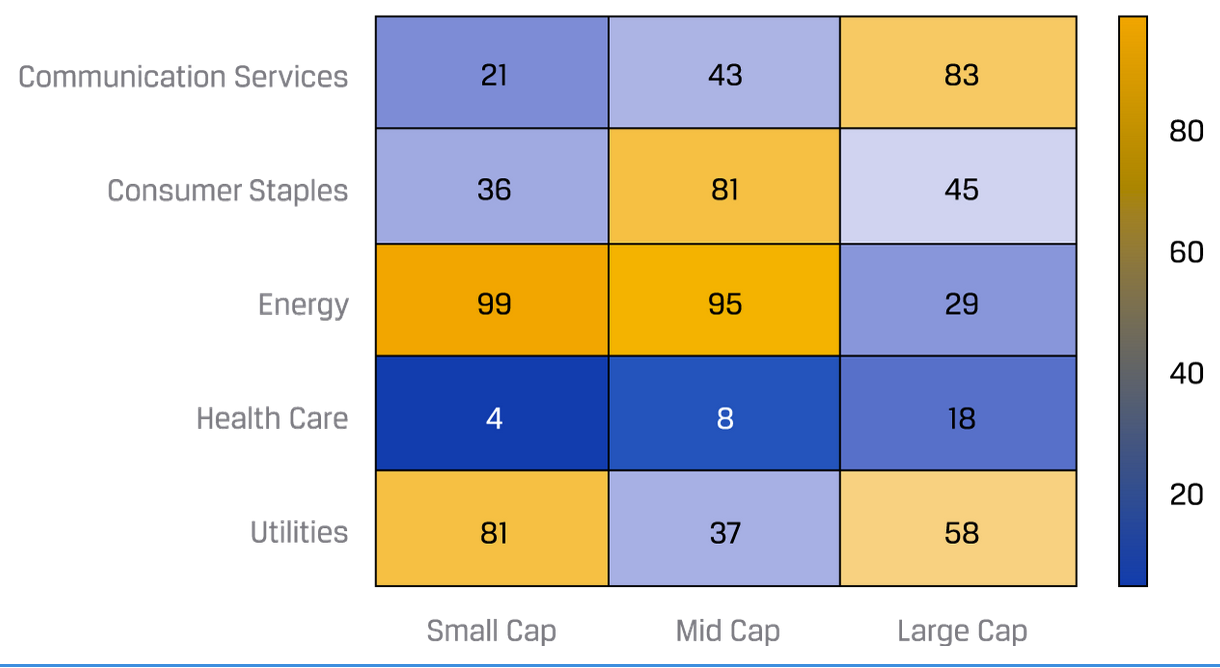
看图时需要注意以下潜在问题:
- 选错类型
- 选择性plot data,比如特意缩短time span来突出一个不是普遍现象的trend
- y轴不是从0开始,显得倍数大
- 坐标轴错误scale,使得图像压缩
Measure of central tendency and location
如果statistics总结了一个population里的所有possible observations,那就叫做parameter;如果总结的是population的subset,那就是sample statistics。
Central tendency的有以下常见描述:
- arithmetic mean 算术平均数
- median 中位数
- mode 众数
- weighted mean 加权平均数
- geometric mean 几何平均
- harmonic mean 调和平均数
方差 deviation ;偏度 skewness ;峰度 kurtosis。更大的峰度代表尾巴更长。
Trimmed mean就是去掉一定比例的最高最低值再算平均;比如5% trimmed mean就是去掉最高和最低各2.5%之后。
Winsorized mean:95% winsorized mean 将排列在2.5%以下的value提升成(等于或高于)2.5%处的值,将排列在97.5%以上的value降低成(等于或低于)97.5%处的值。
众数:只有一个的时候数据集叫Unimodal;两个的话是bimodal;三个是trimodal。
加权平均数:对于portfolio来说,正的权重说明是long头寸,负的short头寸。
几何平均就是n个值乘积的n次方根。所有值都应该是大于等于0才能算。在收益率的场景下有可能是负数,所以一般会给每期的值+1之后算几何平均,再把结果-1。收益率的几何平均值可以看作是compound return rate,着重于多周期;数学平均则是单周期视角。
调和平均数:
对于X是ratio或者rate的时候比较有用;能够更好地减少极端值的影响。
如果有负数,也是跟几何平均值的处理一样先加1变成非负的算出结果再减1。
从数学上来说,数学平均数✖️调和平均数=几何平均数。
quantile
四分位数quartile,五分位数quintile,十分位数decile,百分位数percentile。以及yth percentile。
Interquartile range 就是四分位数中Q3和Q1之间的差。
如果有n个observation,那么确定哪个是第yth分位数的公式:
比如想知道11个数中的75%分位,就是 $L_{75}=(11+1)\times \frac{75}{100} = 9$, 代表着升序排列第9个数是这个dataset的75%分位数。
如果 $L_y$ 不是整数,就用它前后的两个数做线性插值。
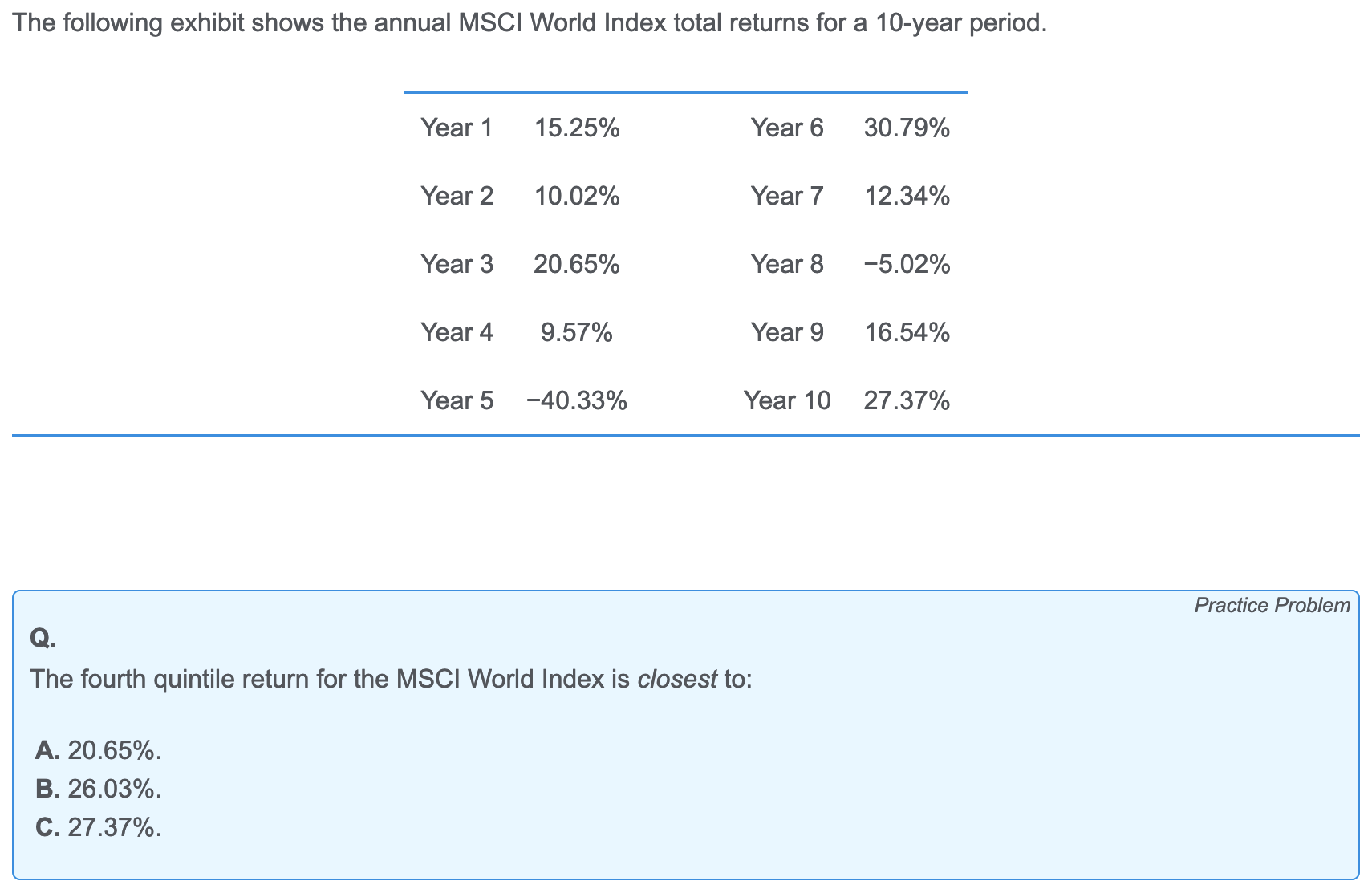
Box and whisker plot:
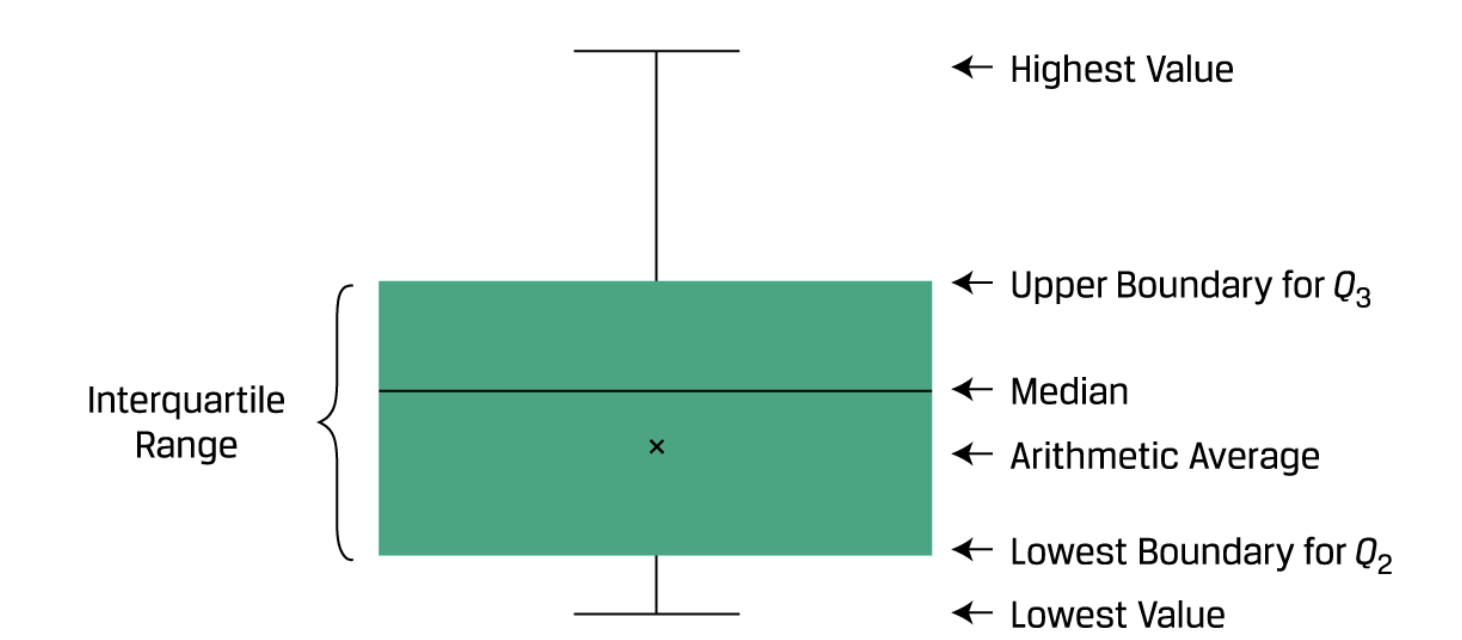
有的时候fences不是用极端值来画,比如有的是用1.5倍IQR来画:

Dispersion
Range,最大值-最小值。
Mean absolute deviation:
Sample Variance:
因为方差和标准差是表示样本与平均数之间的离散程度,所以通常会把平均数也写出来。对于时间序列百分比变化,可以再多写一个几何平均数。此外,几何平均数和方差之间有:
Downside deviation
根据target return(也可以是其他数据)计算的标准差,又称 target semideviation。拿投资来说,有的时候更关心的是回报率不能满足要求的情况,对于超过的就没那么感兴趣;这个指标就是满足这样的需求的。首先确定一个target回报率,然后:
其中 $X_i$ 只拿小于target的;n依旧是全部observation的数量。
Coefficient of Variation
如果不同数据集的平均数显著不同或者单位不同,原版的标准差可能很难直观对比离散程度,所以有了这个指标:
但是如果平均数是负的,就没有意义了。