Cfa笔记interest Rates、pv、fv

于 2024-02-06 发布

Interest rate

有三个角度去理解：

  1. Required rates of return：使得投资者选择这项投资所需要的rate
  2. discount rate：使得FV折现后等于PV的rate
  3. opportunity costs：如果投资者现在consume了这笔钱（而不是invest的话）所损失的rate

有五个构成部分：

  1. Real risk-free interest rate
  2. Inflation premium, 加上第一个就是nominal risk-free interest rate。比如美国国债指的就是这种
  3. Default risk premium
  4. Liquidity premium，可以理解为“容不容易卖出去”，容易卖就低，难卖就高
  5. Maturity premium，期限越长market value对市场利率的变动的敏感性越高

对于公式 $FV_N=PV(1+r)^N$, 需要注意r和N必须要是相同时间尺度（年对年，月对月）；如果每年复利次数大于1（设为m），而年利率为 $r_s$ ：

$$ FV_N=PV(1+\frac{r_s}{m})^{mN} $$

如果m趋向于∞，就叫做continuous compounding，公式是：

$$ FV_N=PVe^{r_sN} $$

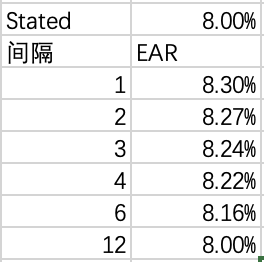
EAR

多数时候标明的（stated）利率都是年利率，但是如果compound period不是1年，effective annual rate (EAR)就会不同，比如：$(1+(8\%/12))^{12}≈1.083$

$$ EAR = \begin{cases} (1+\frac{r_s}{m})^m - 1 & \text{if } \text{discrete} \\ e^{r_s} - 1 & \text{if } \text{continuous} \end{cases} $$

对于continuous的： $FV=PV\times e^{r_sN}$ 给出EAR也可以反算periodic rate。

Alt text

现金流

常见名词：

  1. annuity（年金） 1
  2. ordinary annuity：a first cash flow that occurs one period from now的年金
  3. annuity due：a first cash flow that occurs immediately
  4. perpetuity：永久年金（但是一个周期之后才会出现第一次付款）

annuity due的折现次数会比ordinary annuity少一次。

Ordinary Annuity

通用公式：

$$ FV=\Sigma^N_{n=1}{A_n \times (1+r)^{N-n}} $$

如果每年的金额 $A_n$ 相同，就可以简化 2 为：

$$ FV_N = A[\frac{(1+r)^N-1}{r}] $$

PV就是反过来算。

perpetuity

$$ PV=\frac{A}{r} $$

如果开始时间不是今天（t=0），比如t=2才付第一次，那就先用公式算t=1的时候的perpetuity的PV，然后再将那个PV再折现回t=0。

A和r是要相同周期的，比如A是季度付，那r也要用年利率除以4

FV、PV、annuity等价性

只要站在同一个时间点上来计算，FV、PV和年金就是等价的。由此也就有了The Cash Flow Additivity Principle：the idea that amounts of money indexed at the same point in time are additive。

经典题目

两个perpetuity，但是买的是t=1付第一次，发行的是t=5付第一次，金额相同。由于前四期存在现金差值，类似于ordinary annuity，所以存在PV可以算。

将PV和FV改成某两年的销售额，计算compound growth rate。

贷款，给出现在要借的钱（PV），给出年利率，给出compound方式（比如月），给出年限，求月供。（等同于问年金的金额是多少才能让PV等于现在要借的钱）。 3注意，对于这种计算PMT的，需要设置BA II Plus的C/Y和P/Y，否则算的是不对的。

这个题要先算出EAR然后再算年然后年除以12得到月，不能够算天然后折算成月。 Alt text

BA II Plus的年金PV和FV计算

期数N，利率I/Y（输入就是百分比，比如8%就输入8）：

  1. 算PV，就输入PMT（每年付款），然后FV输入0
  2. 算FV，就输入PMT，然后PV输入0
  3. 算PMT，记得PV和FV的符号不能一样

题目：

Jill Grant is 22 years old (at t = 0) and is planning for her retirement at age 63 (at t = 41). She plans to save $2,000 per year for the next 15 years (t = 1 to t = 15). She wants to have retirement income of $100,000 per year for 20 years, with the first retirement payment starting at t = 41. How much must Grant save each year from t = 16 to t = 40 in order to achieve her retirement goal? Assume she plans to invest in a diversified stock-and-bond mutual fund that will earn 8 percent per year on average.

提示：可以站在t=15或者t=40两个节点来计算；任意时间点上，之前的钱的FV要等于未来的钱的PV。

  1. 年金的“年”并不意味着现金流的period是年；这个词指的是连续的固定间隔支付的现金流。 ↩

  2. 等比数列求和 $S_n=a \times \frac{1-r^n}{1-r}$, 其中 a=1,r=(1+r) ↩

  3. 教材中会提到lump sum可以产生annuity所需的付款；通过这个抵押贷款的例子理解，银行在你身上一次性存这个钱，而年金就是月供，最终FV就是0，实现了利率。 ↩

目录